A pendulum of length 1m hangs from an inclined wall. Suppose that this pendulum is released at an initial angle of 10∘ and it bounces off the wall elastically when it reaches an angle of −5∘ as shown in the figure. Take g=π2m/s2. The period of this pendulum is (in second)

2/3
3/2
3/4
4/3
The correct Answer is:D
We take θ=(10∘)cos(πt), calculate t when θ=−5∘. This gives t=2/3(s). The period is 2 times this.
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
Knowledge Check
The l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
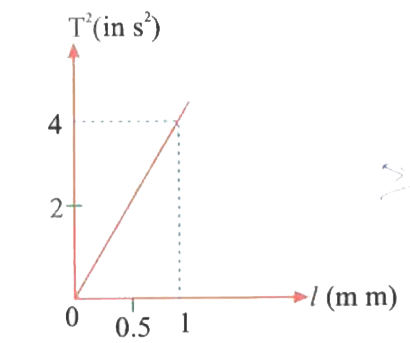 A1sB1.2 sC√2 sD1√2s
A1sB1.2 sC√2 sD1√2sThe acceleration due to gravity at a place is π2m/s2. Then, the time period of a simple pendulum of length 1 m is
A2πsB2πsC2sDπsA simple pendulum of length 1m has bob of mass 100 g. It is displaced through an angle of 60∘ from the vertcal and then released. The kinetic energy of bob when it passes through the mean position is
A0.25JB0.5JC1.0JD1.4J
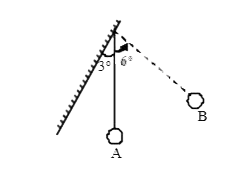
A pendulum of length 10 cm is hanged by wall making an angle 3∘ with vertical. It is swinged to position B. Time period of pendulum will be
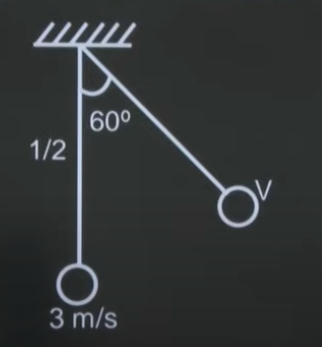
View SolutionA simple pendulum of length 1/2m has initial speed 3m/s when pendulum mass is at lowermost point. What will be the speed pf pendulum mass, when the string of pendulum makes an angle of 600 with vertical.
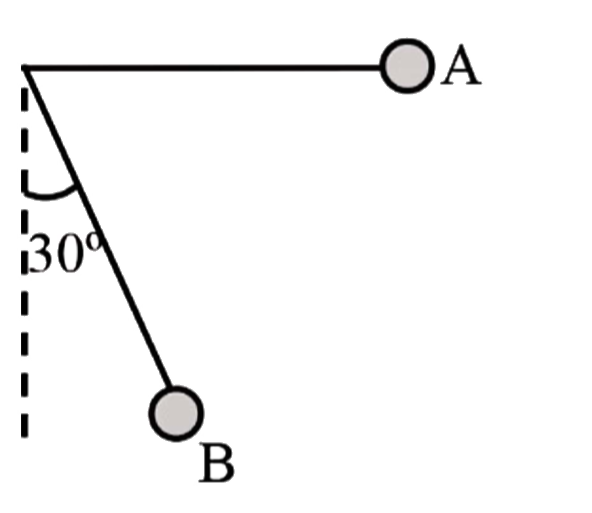
View SolutionA simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
View SolutionA pendulum is formed by pivotting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.

The time period of this pendulum when d = L/2 will be
View SolutionA pendulum of length = 1 m is released from 0 = 60º. The rate of change of speed of the bob at = 30º is: (g = 10 m/s2)

View Solution

