If a hole is punctured in a tire, the gas inside will gradually leak out of it. Let's assume the following : the area of the hole is A, the tire volume is V, and the time it takes for most of the air to leak out of the tire be t. This time can be expressed in terms of the ratio A/V, the temperature T. the Universal gas constant R, and the mass of the gas molecules inside the tire, m. Under these assumptions, we can use dimensional analysis to find an estimate for t. Assuming this estimate to be correct, if the mass of air within a tyre is increased by 70%, the absolute tyre temperature increased by 20%, while the area of the punctured hole is doubled (but still small) then the time in which a tyre will go flat will
increased by 10%
increase by 25%
decrease by 25%
decrease by 40%
The correct Answer is:D
Using dimensional analysis or otherwise t=VA√mRT× some numerical factor
Substituting the values we get t't=12√1.71.2≈0.6
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
A vessel of volume V contains ideal gas at the temperature T0∘C. After a portion of the gas the been let out , the pressure in the vessel decreased by Δp ( the temperature remaining constant). . Find the mass ofthe re.leased gas.The gas density under the noraml conditions ρ
View SolutionLok at the barometer shown in the figure. If a small hole is developed in the wall of the tube at point A, will the mercvuty leak out of it?
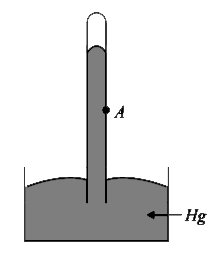
View Solution
Knowledge Check
The tired place .
AStrolledBscurriedCparadedDploddedThe volume of one mole of an ideal gas changes from V to 2V at temperature 300 K. If R is universal gas constant, then work done in this process is
A300 Rln2B600 Rln2C300 ln2D600 ln2If γ is the ratio of specific heats and R is the universal gas constant, then the molar specific heat at constant volume CV is given by
AγRB(γ−1)RγCRγ−1DγRγ−1
If P is the pressure,V the volume,R the gas constant,k the Boltzmann constant and T the absolute temperature,then number of molecules in the given mass of the gas is given
View SolutionThe equation of state of a real gas is given by (P+aV2)(V−b)=RT
where P, V and T are pressure, volume and temperature resperature and R is the universal gas constant. The dimensions of the constant a in the above equation is
View SolutionA gas is enclosed in a vessel at a pressure of 2.5atm. Due to leak in the vessel., after some time the pressure is reduced to 2atm, temperature remaining unchanged. The percentage of gas that has leaked out is
View SolutionThe rate of leak from a hole in a tank is :
View SolutionThe pressure P, Volume V and temperature T of a gas in the jar A and the other gas in the jar B at pressure 2P, volume V/4 and temperature 2T, then the ratio of the number of molecules in the jar A and B will be
View Solution

