The moment of inertia of a uniform solid regular tetrahedron of mass m and edge a, about its symmetry axis (i.e and axis passing through on evertex and the centre of the opposite face) is:
ma2/10
3ma2/10
ma2/15
ma2/20
The correct Answer is:D
For an equilateral triangle of side a, moment of inertia is ma112about an axis passing through its CM and perpendicular to plane - the result of the integration is similar to that of a solid cone along its axis: a factor of 3/5
1=35(ma212)
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
The moment of inertia of a uniform solid regular tetrahedron of mass m and edge a, about its symmetry axis (i.e and axis passing through on vertex and the centre of the opposite face) is:
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
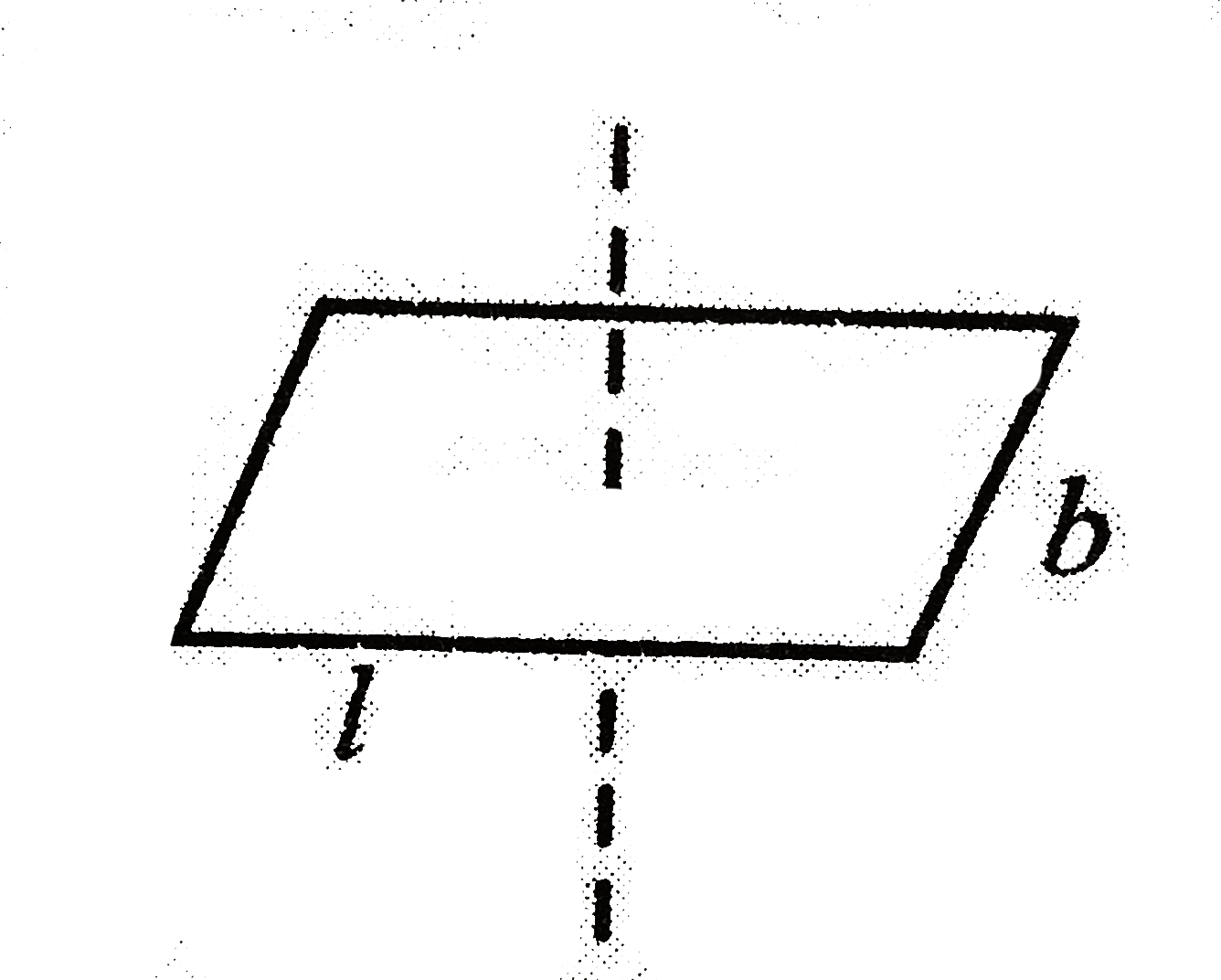
View Solution
Knowledge Check
The moment of inertia of a hollow cubical box of mass M and side a about an axis passing through the centres of two opposite faces is equal to.
A5Ma23B5Ma26C5Ma212D5Ma218
Find the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.

View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionFind moment of inertia of a uniform rectangular plate (mass m) about axis AB lying in its plane and passing through center as shown in the figure.

View SolutionThe moment of inertia of a uniform cicrular disc about its diameter is 200gcm2. Its moment of inertia about an axis passing through its centre and perpendicular to its circular face is
View SolutionThe moment of inertia of a solid cylinder of density ρ, radius of base r, and height h about an axis passing through its centre of mass and parallel to length is
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View Solution

