A person starts with a speed of √(0.5gr) at the top of a large frictionless spherical surface, and slides into the water below (see the drawing). Then , the person
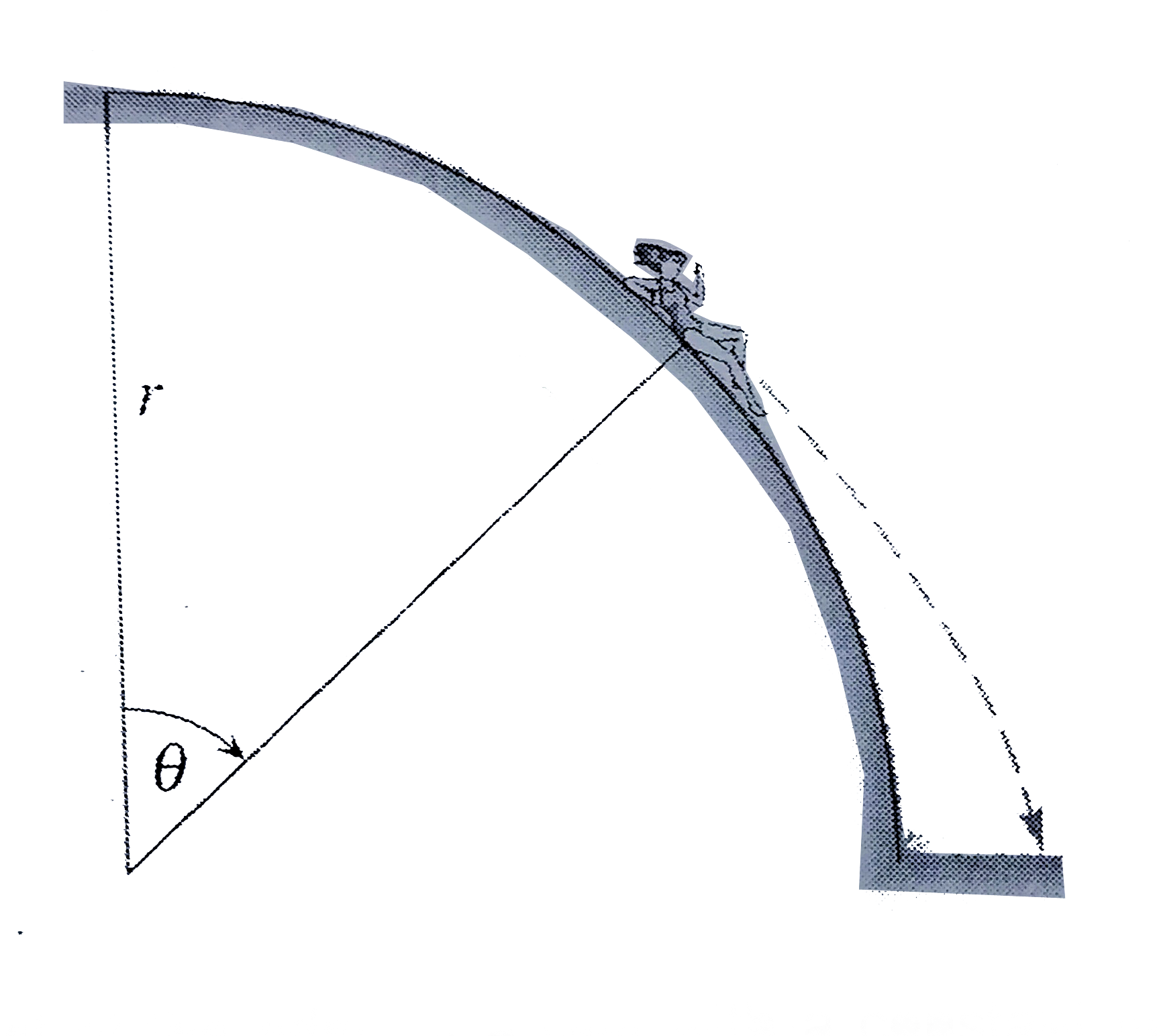
loses contact when cosθ=1/3
slides through a height of r/6 before losing contact
slides through a height of r/3 before losing contact
never loses contact with the surface
The correct Answer is:B
The normal reaction vanishes when the person loses contact with the surface:
mv2/r=mgcosθ,
Conservation of energy gives,
1/2mv2+mgrcosθ=1/2mu2+mgr, where u2=0.5gr
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
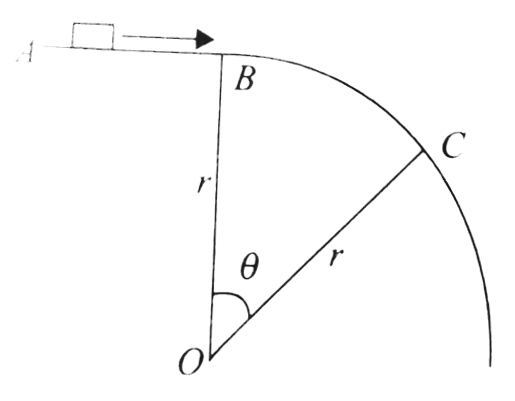
A small block slides with velocity v0=0.5√gr on the horizontal frictiohnless surface as shown in the fig. the block leaves the surface at point C. The angle θ in the figure is:
View SolutionA small block slides with velocity v0=0.5√gr on the horizontal frictionless surface as shown in the figure. The block leaves the surface at point C. The angle θ in the figure is cos−1(x)y. Find (x+y).
'(##CEN_KSR_PHY_JEE_C07_032_Q21##)'
View Solution
Knowledge Check
A particle is projected with a speed v0=√gR. The coefficient of friction the particle and the hemi- spherical plane is μ=0.5 Then , the acceleration of the partical is
 AgB√5g2C√2gDnone of these
AgB√5g2C√2gDnone of theseThe distance between points P and Q is 485 km. If a person starts from point P with the speed of 60 km/h and another person is running with a certain speed from point Q and they both meet after 2.5 hours then find the speed of the person who starts from point Q
A140 km/hB126 km/hC156 km/hD134 km/hA ball is thrown from a point with a speed 'v^(0)' at an elevation angle of θ . From the same point and at the same instant , a person starts running with a constant speed 'v0'2 to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection θ ?
ANoByes, 30(∘)Cyes,60(∘)Dyes ,45(∘)
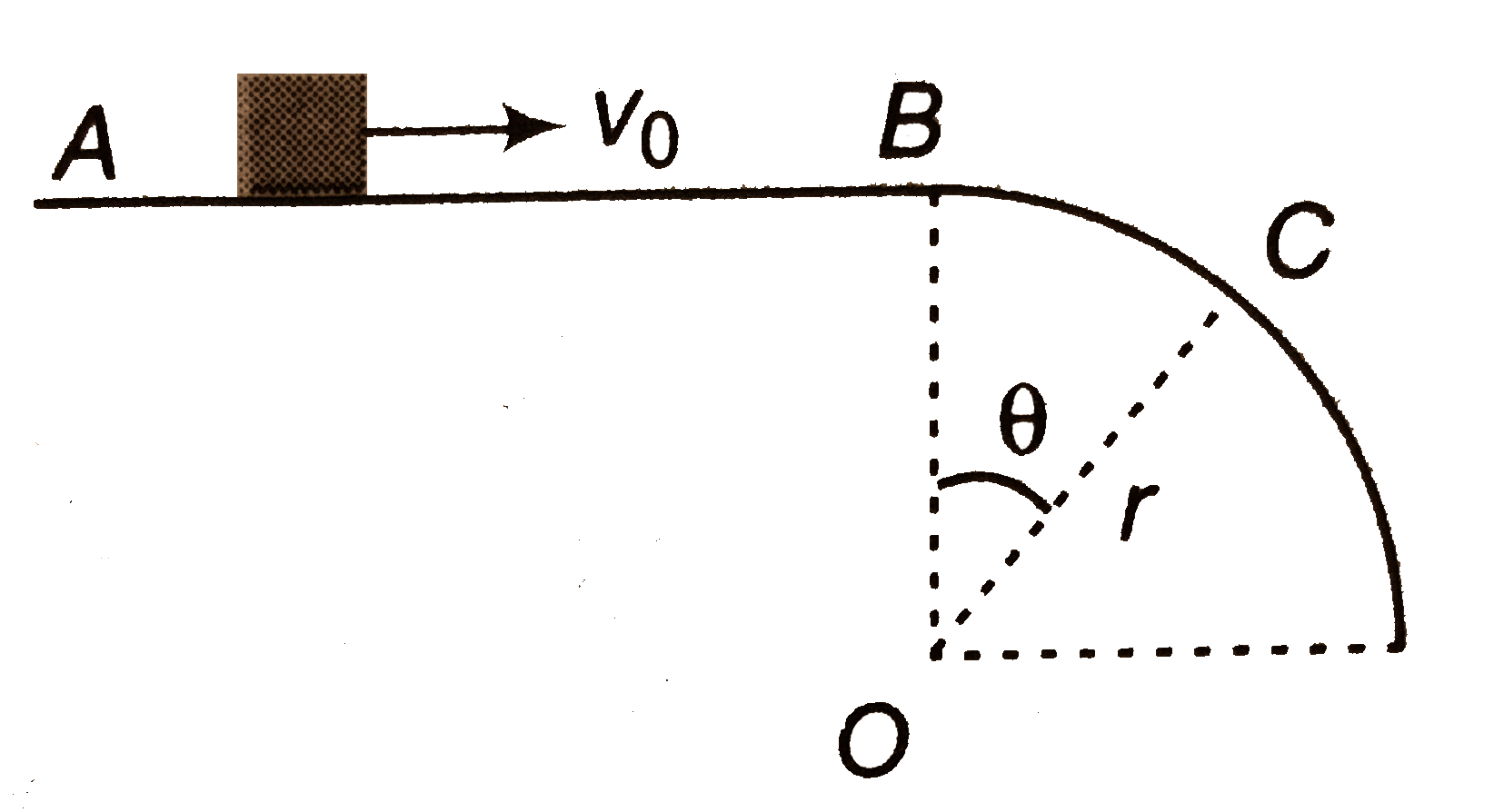
A small block slides with velocity 0.5√gr on the horizontal frictionless surface as shown in the figure. The block leaves the surface at point C . Calculate angle θ in the figure.
View SolutionThe huge advantage of using the conservation of energy instead of Newton's laws of motion is that we can jump from the initial state to the final state without considering all the intermediate motion. Here is an example. In Fig. 8-25, a child of mass m is released from rest at the top of a water slide, Assuming that the slide is frictionless because of the water on it, find the child's speed at the bottom of the slide.
View SolutionSome persons hired a boat for 3 hours. The river flows at a speed of 2.5km/hr and the speed of the boat is 7.5km/hr relative to the water. They start from the port rowing along the river flow and they want to be back in 3hrs.Find the value of a if distance travelled by them is (4+a)km
View SolutionA ball is thrown from a point with a speed V0,at an angle of projection θ.From the same point and at the same instance a person starts running with a constant speed V0√2 to catch the ball will the person be able to catch the ball? If yes, what should be the angle of projection
View SolutionA spherical body of radius R is allowed to roll down on an incline with out slipping and it recheas with a speed v0 at the bottom. The incline is then made smooth by waxing and the body is allowed top slide without rolling and now the speed attained is 54v0 The radius of gyration of the body about an axis passing through the centre is
View Solution

