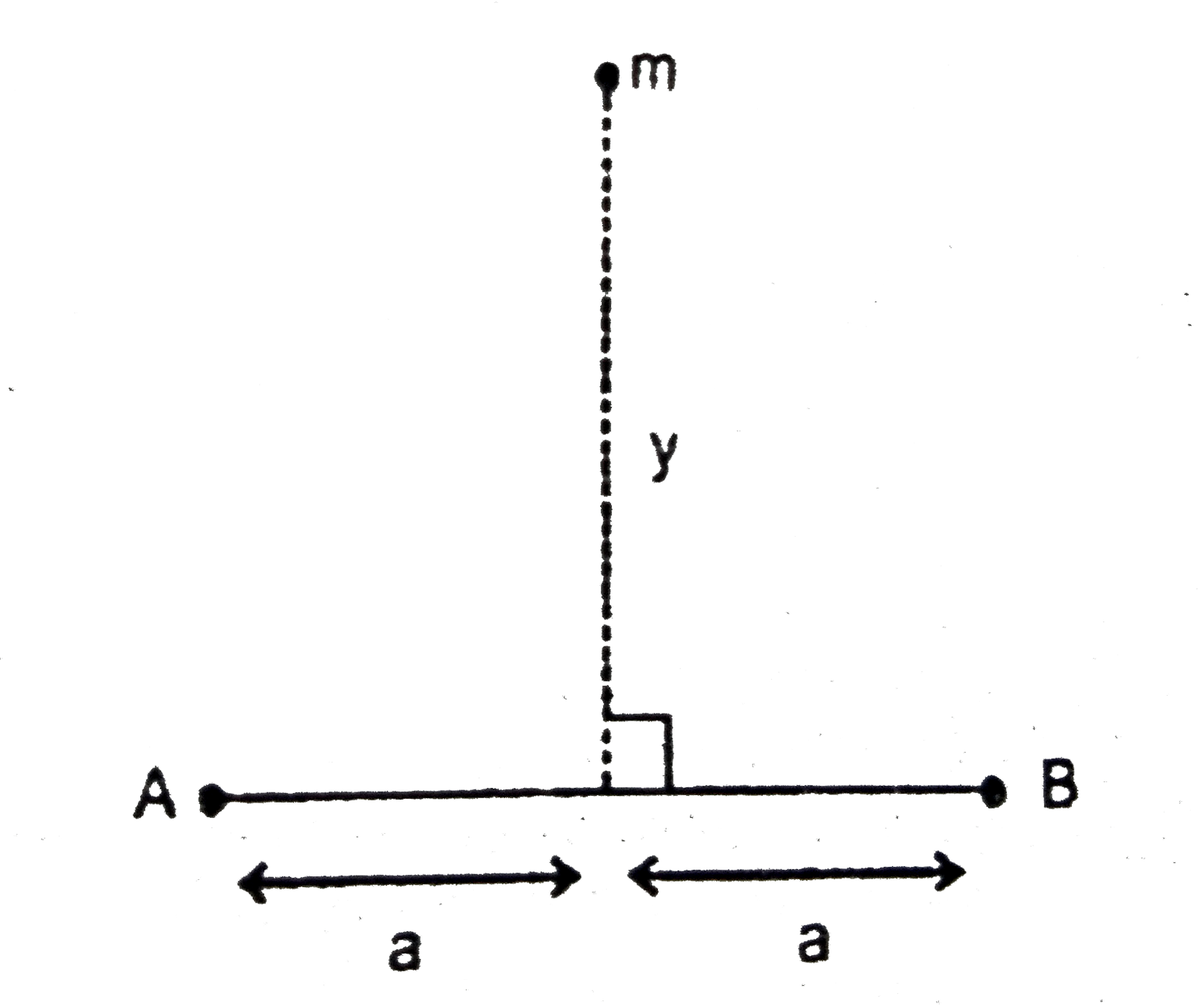
Potential energy of a particle of mass m, depends on distance y from line AB according to given relation U=K√y2+a2, where K is a positive constant. A particle of mass m is projected from y=√3 towards line AB. (perpendicular to it) then minimum velocity so that it connot return to its initial point is √KaNm, calculate N.
The correct Answer is:1
Ui+ki=Uf+kf
K2a+12mV20=Ka
mV202=K2a⇒v0=√Kam
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Physics
Explore 775 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 2
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
Similar Questions
A particle of mass m moves in a striaght line . If v is the velocity are distance x from a fixed point on the line varies as v2=a−bx2, where and b are +ve constants, then
View SolutionIn a region, potential energy varies with X as U(x)=30−(x−5)2 Joule, where x is in meters. A particle of mass 0.5 kg is projected from x=11 m towards origin with a velocity 'u' . u is the minimum velocity, so that the particle can reach the origin. (x=0). find the value of u/2 in meter/second. (Take √44=6.5)
View Solution
Knowledge Check
The potential energy of a particle varies with distance x from a fixed origin as U=A√xx2+B, where AandB are dimensional constants , then find the dimensional formula for AB.
A[ML11/2T−1]B[ML11T−2]C[ML7/2T−2]D[ML11/2T−2]The kinetic energy K of a particle moving in a straight line depends on the distances as K=as2. The force acting on the particle is
(where a is a constant)A2asBasC2aD√as2A particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression U=ax2−bx, where a and b are positive constant. The particle will perform.
Aoscillatory motion but not simple harmonic motion about its mean position for small displacementsBsimple harmonic motion with time period 2π√8a2mb4 about its mean position for small displacementsCneither simple harmonic motion nor oscillatory about its mean position for small displacementsDnone of the above
The velocity of the particle of mass m as a function of time t is given by v=Aω.cos[√Kmt] , where A is amplitude of oscillation. The dimension of AK is
View SolutionThe potential energy of a particle of mass 1 kg in a conservative field is given as U=(3x2y2+6x) J, where x and y are measured in meter. Initially particle is at (1,1) & at rest then:
View SolutionThe potential energy of a particle is determined by the expression U=α(x2+y2), where α is a positive constant. The particle begins to move from a point with coordinates (3,3), only under the action of potential field force. Then its kinetic energy T at the instant when the particle is at a point with the coordinates (1,1) is
View SolutionThe potential energy of a particle of mass 2 kg moving in a plane is given by U=(−6x−8y)J. The position coordinates x and y are measured in meter. If the particle is initially at rest at position (6, 4)m, then
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View Solution

