In a region, potential energy varies with X as U(x)=30−(x−5)2 Joule, where x is in meters. A particle of mass 0.5 kg is projected from x=11 m towards origin with a velocity 'u' . u is the minimum velocity, so that the particle can reach the origin. (x=0). find the value of u/2 in meter/second. (Take √44=6.5)
Draw U v/s x graph. There is a maxima of potential energy between x = 11 to x = 0. So to bring the particle from x = 11 to x = 0, the particle has to cross the maxima (x = 5) and to just cross the point x = 5, velocity at x = 5 should be 0+
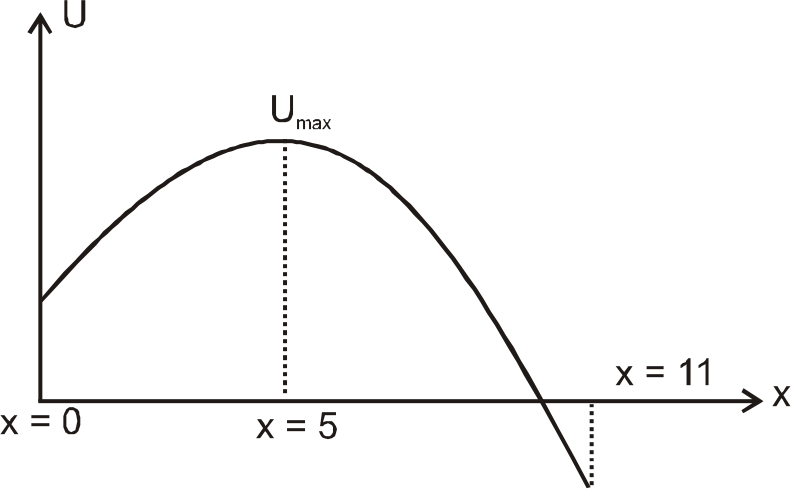
⇒ Applying energy conservation between x=11 to x=5
ki+Ui=kf+Uf
12(0.5)u2+(30−(11−5)2)=0++(30−(5−5)2)
u=12m/sec⇒u2=6m/sec
Topper's Solved these Questions
Similar Questions
Potential energy of a particle along x-axis varies as U = - 30 + (X−2)2, where U is in joule and x is in meter. Hence the particle is in
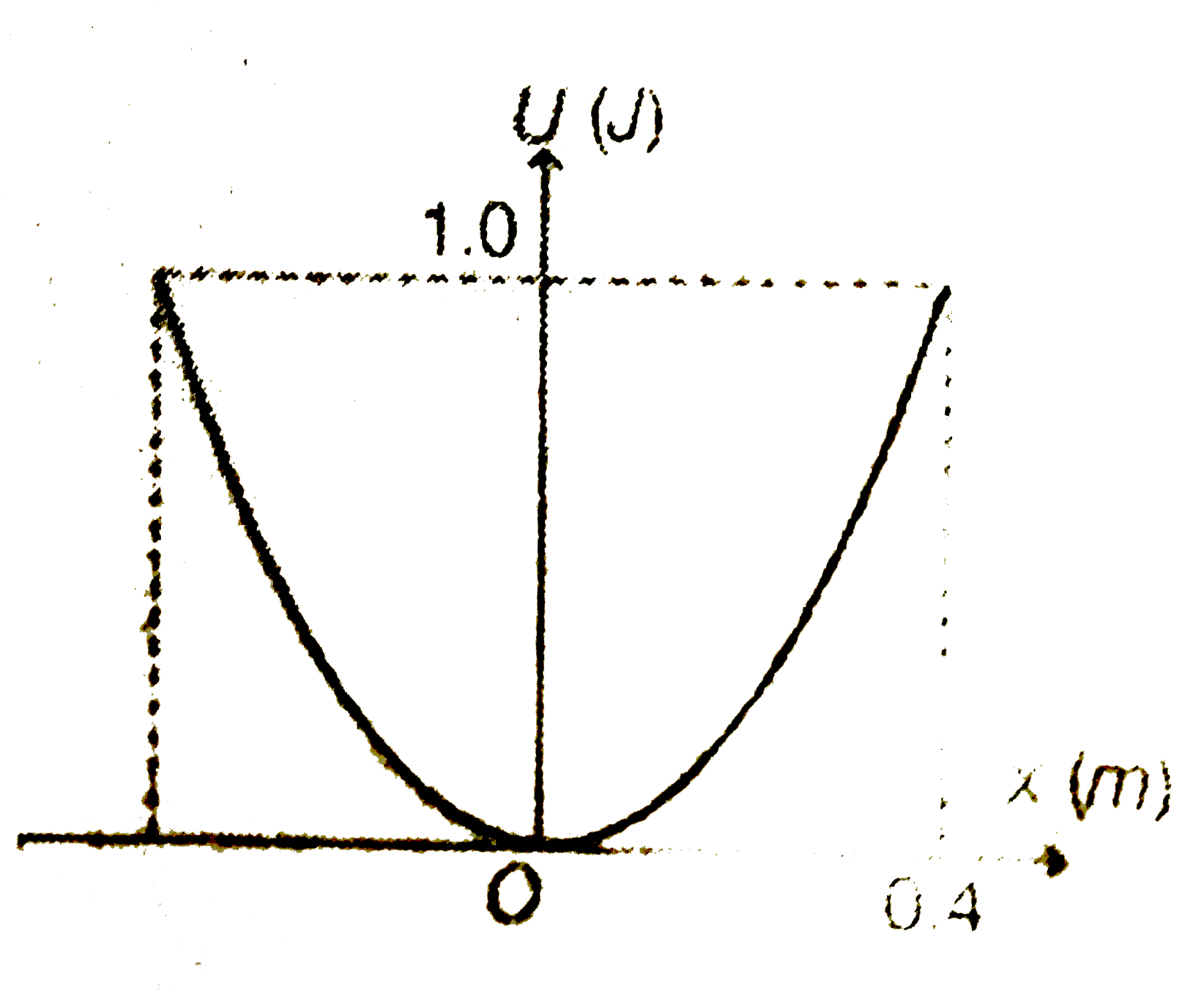
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
View Solution
Knowledge Check
The potential energy of a particle is given by formula U=100−5x+100x2,whereU and are .
AAt 0.05m form the origin is 50 ms^(2).BAt 0.05 m from the mean position is 100 ms^(2).CAt 0.05 m feom the origin is 150 ms^(2).DAt 0.05m from the mean position is 200ms−1The potential energy of particle of mass 1kg moving along the x-axis is given by U(x)=16(x2−2x) J, where x is in meter. Its speed at x=1 m is2m/s. Then,
Athe motion of the particle is uniformly acceleratedBthe motion of the particle is periodic but not simple harmonic.Cthe motion of the particle is simple harmonic having equilibrium position at x=1mDkinetic energy of the particle is conservedThe potential energy of a particle of mass 1 kg moving in X-Y plane is given by U=(12x+5y) joules, where x an y are in meters. If the particle is initially at rest at origin, then select incorrect alternative :-
AMagnitude of its acceleration is 13m/s2BIt never crosses y-axisCIt never crosses x-axisDIt moves in a circle.
The potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionA particle can move along x axis under influence of a conservative force. The potential energy of the particle is given by U=5x2–20x+2 joule where x is co-ordinate of the particle expressed in meter. The particle is released at x = –3 m (a) Find the maximum kinetic energy of the particle during subsequent motion. (b) Find the maximum x co-ordinate of the particle.
View SolutionA conservative force acts on a 4 kg particle in x direction. The potential energy U(x) is given by U(X)=40+(x–6)2, where x is in metre. If it is given that at x = 8 m, KE is 30 J then find the maximum KE of the particle.
View SolutionThe potential energy of a particle varies with x according to the reltiaon U(x) =x2−4x. The point x =2 is a point of
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View Solution

