A particle of mass m=1kg is lying at rest on x-axis, experiences a net force given by law F=x(3x−2) Newton, where x is the x-coordinate of the particle in meters. The magnitude of minimum velocity in negative x-direction to be imparted to the particle placed at x=4 meters such that it reaches the origin is √P27m/s. find the value of P.
The particle is at equilibrium at x=0 and x=2/3
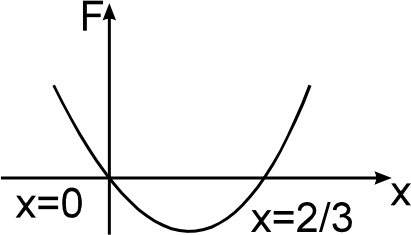
The minimum speed imparted to the particle should be such that it just reaches x=2/3 from there on it shall automatically reach x=0
12mv2=−∫2/34Fdx=−∫2/34x(3x−2)dx=130027 or v=√260027m/s
Topper's Solved these Questions
Similar Questions
A particle of mass m=1kg lying on x-axis experiences a force given by law
F=x(3x−2) Newton.
Where x is the x-coordinate of the particle in meters.
−−−−−−−−−→x=0x=4
(a) Locate the point on x-axis where the particle is in equilibrium.
(b) Draw the graph of variation of force F (y-axis) with x-coordinate of the particle (x-axis). Hence or otherwise indicate at which positions the particle is in stable or unstable equilibrium.
(c ) What is the minimum speed to be imparted to the particle placed at x=4 meters such that it reaches tha origin.
View SolutionA particle of mass m=1kg lying on x-axis experiences a force given by law
F=x(3x−2) Newton.
Where x is the x-coordinate of the particle in meters.
−−−−−−−−−→x=0x=4
(a) Locate the point on x-axis where the particle is in equilibrium.
(b) Draw the graph of variation of force F (y-axis) with x-coordinate of the particle (x-axis). Hence or otherwise indicate at which positions the particle is in stable or unstable equilibrium.
(c ) What is the minimum speed to be imparted to the particle placed at x=4 meters such that it reaches tha origin.
View Solution
Knowledge Check
The velocity of a particle moving along x-axis is given as v=x2−5x+4 (in m/s) where x denotes the x-coordinate of the particle in metres. Find the magnitude of acceleration of the particle when the velocity of particle is zero?
A0m/s2B2m/s2C3m/s2DNone of theseThe potential energy φ, in joule, of a particle of mass 1kg, moving in the x-y plane, obeys the law φ=3x+4y, where (x,y) are the coordinates of the particle in metre. If the particle is at rest at (6,4) at time t=0, then
AThe particle has constant accelerationBThe work done by external forces from the position of rest to the instant the particle crossing x-axis is 25JCThe speed of the particle when it crosses the y-axis is 10ms−1DThe coordinates of the particle at time t=4s are (−18,−28) (in m)A particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
AzeroB42 mCInfiniteDNone of these
A particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
View SolutionA particle starts moving in a straight line from rest with an acceleration (inm/s2) given by : a=12√x, where x is the distance travelled by the particle (in meters ) The velocity of the particle at the instant when its acceleration is 48m/s2 is .......m/s
View SolutionA particle moves along the X-axis from x=0→x=5m under the influence of a force given by F=(7−2x+3x2). Find the work done in the process.
View SolutionThe potential energy of a particle of mass 1 kg moving in X-Y plane is given by U=(12x+5y) joules, where x an y are in meters. If the particle is initially at rest at origin, then select incorrect alternative :-
View SolutionA particle of mass 5 kg moving in the x-y plane has its potential energy given by U=(−7x+24y)J where x and y are in meter. The particle is initially at origin and has a velocity →i=(14ˆi+4.2ˆj)m/s
View Solution

