A hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.

When the insect is at point ‘P’ of the hemispherical bowl the acceleration of bowl is :
Zero
(mM+m)v2Rcosθ horizontally towards left
(MM+m)v2Rsinθ horizontally towards right
(mM+m)v2Rcosθ horizontally towards right
Momentum of system in horizontal will remain conserved, so
MV=m(vsinθ−V)
⇒V=mvM+msinθ
dVdt=mvM+mcosθ(dθdt)
(dVdt)=(mM+m)v2Rcosθ
Topper's Solved these Questions
Similar Questions
A hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.
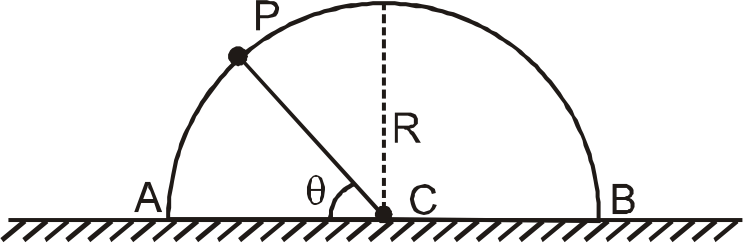
When insect at point ‘P’ on the bowl the displacement of centre of mass of the system (bowl + insect) is :
View SolutionFind the total surface area of a hemispherical bowl of radius 5 cm .
View Solution
Knowledge Check
A hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.
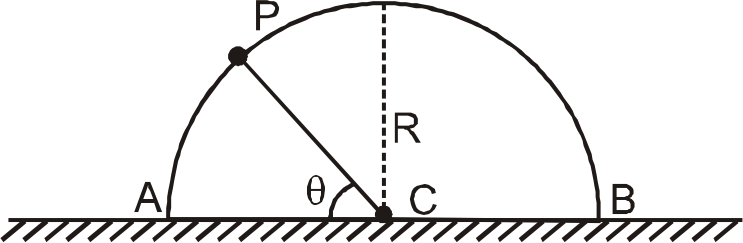
When the insect reaches point ‘P’ of the hemisphere the displacement of hemisphere w.r.t. ground is :AZeroBMR(M+m)(1−cosθ) horizontally towards leftCmR(M+m)(1−cosθ) horizontally towards leftDmR(1+cosθ)(M+m)(1+cosθ)A strip of wood mass M and length l is placed on a smooth horizontal surface. An insect of mass m starts from rest at one end of the strip and walks to the other end in time t, moving with a constant speed.
AThe speed of the insect as seen from the ground is <lt.BThe speed of the spring as seen from the ground is lt(MM+m)CThe speed of the strip as seen from the ground is lt(mM+m)DThe total kinetic energy of the system is 12(m+M)(lt)2.A strip of wood of mass M and length l is placed on a smooth horizontal surface. An insect of mass m starts at one end of the strip and walks to the other end in time t, moving with a constant speed. The speed of the insect as seen from the ground is
Alt(MM+m)Blt(mM+m)Clt(Mm)Dlt(mM)
Find the total surface area of a hemispherical bowl of radius 5cm
View SolutionA hemispherical bowl of radius R is placed upside down on a flat horizontal surface. There is a small hole at the top of the inverted bowl. Through the hole, a liquid of density ρ is poured in. Exactly when the container gets full, water starts leaking from between the table and the edge of the container. Find the mass (m) of the contaienr.
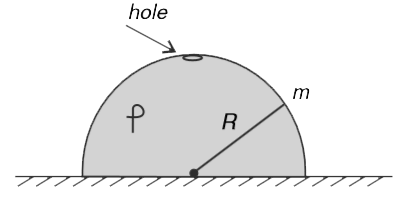
View SolutionA hollow hemispherical bowl of mass m radius R is placed on a smooth horizontal surface. A particle (also of mass m) strikes the hemi spherical bowl at point P and sticks to it. the velocity of particle just after the collision in vertically upwards direction is ku25, where k is an integer. Find k.

View SolutionA hollow hemispherical bowl of thickness 1 cm has an inner radius of 6 cm. Find the volume of metal required to make the bowl.
View SolutionThe radius of a hemispherical bowl is 6 cm. The capacity of the bowl is
(Take π=227)
View Solution

