A particle can move along x axis under influence of a conservative force. The potential energy of the particle is given by U=5x2–20x+2 joule where x is co-ordinate of the particle expressed in meter. The particle is released at x = –3 m (a) Find the maximum kinetic energy of the particle during subsequent motion. (b) Find the maximum x co-ordinate of the particle.
The correct Answer is:(a)Kmax=125J
(b)Xmax=7m
Step by step video, text & image solution for A particle can move along x axis under influence of a conservative force. The potential energy of the particle is given by U = 5x^2 – 20x + 2 joule where x is co-ordinate of the particle expressed in meter. The particle is released at x = –3 m (a) Find the maximum kinetic energy of the particle during subsequent motion. (b) Find the maximum x co-ordinate of the particle. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A long taut string is plucked at its centre. The pulse travelling on it can be described as y(x,t)=e−(x+2t)2+e−(x−2t)2. Draw the shape of the string at time t=0, a short time after t=0 and a long time after t=0.
View SolutionThe potential energy of a particle oscillating along x-axis is given as
U=20+(x−2)2
Here, U is in joules and x in meters. Total mechanical energy of the particle is 36J.
(a) State whether the motion of the particle is simple harmonic or not.
(b) Find the mean position.
(c) Find the maximum kinetic energy of the particle.
View SolutionA particle moving on x - axis has potential energy U = 2 - 20x + 5x^(2) joule along x - axis. The particle is relesed at x = -3 . The maximum value of x will be ( x is in metre)
View SolutionA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
The maximum and minimum values of x, respectively, are
View SolutionA particle of mass m = 1 kg is free to move along x axis under influence of a conservative force. The potential energy function for the particle is U=a[(x/b)^(4)-5(x/b)^(2)] joule Where b = 1.0 m and a = 1.0 J. If the total mechanical energy of the particle is zero, find the co-ordinates where we can expect to find the particle and also calculate the maximum speed of the particle.
View SolutionIn the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
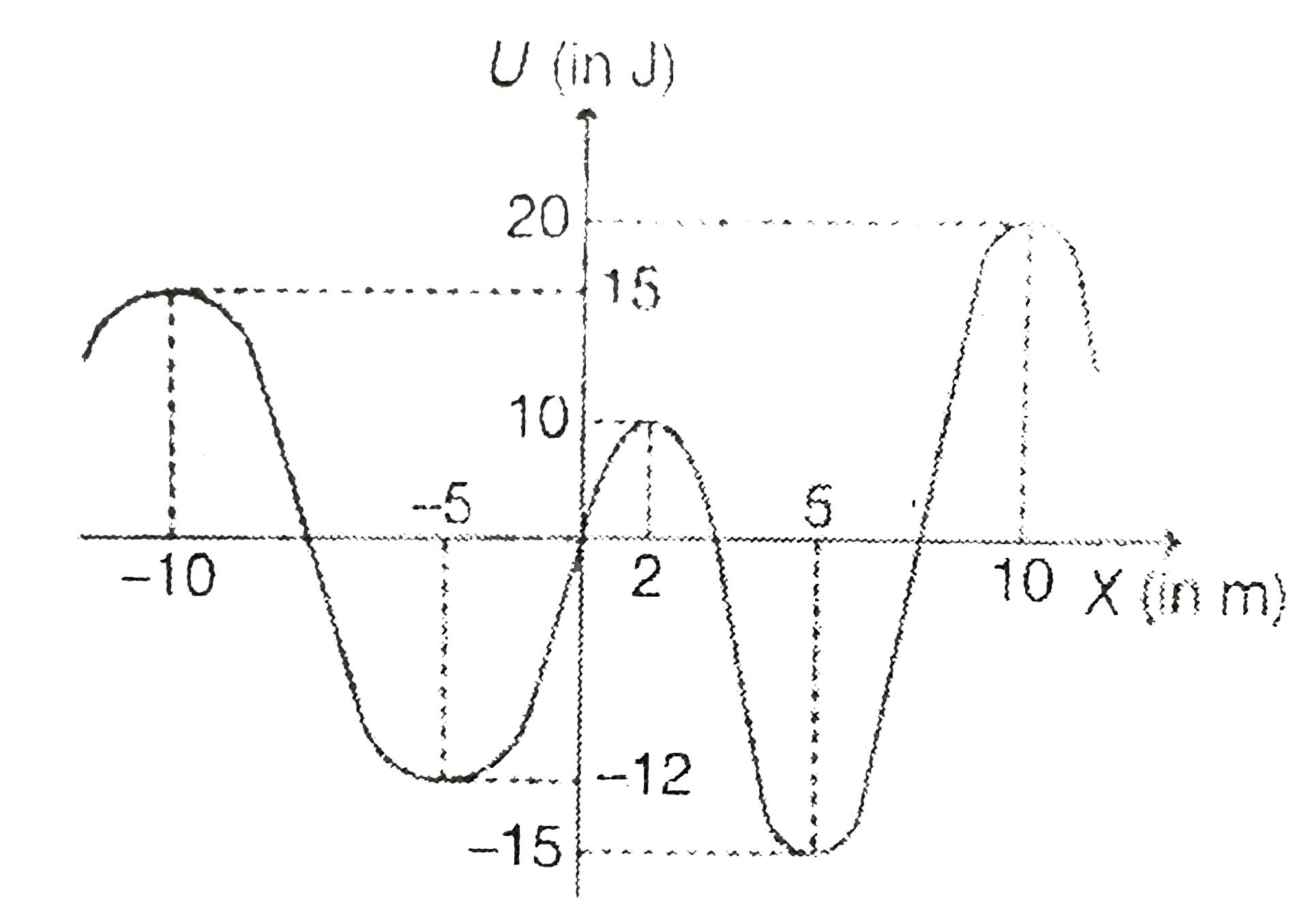
If the particle is released at x=2+Δ where Δ→0 (it is positive), then its maximum speed in subsequent motion will be
View SolutionThe potential energy of a particle of mass 1 kg free to move along x-axis is given by U(x) =(x^(2)/2-x) joule. If total mechanical energy of the particle is 2J then find the maximum speed of the particle. (Assuming only conservative force acts on particle)
View SolutionA single conservative force F(x) acts on a particle that moves along the x - axis. The graph of the potential energy with x is given. At x=5m, the particle has a kinetic energy of 50 J and its potential energy is related to position 'x' as U=15+(x−3)2 Joule where x is in meter. Then:
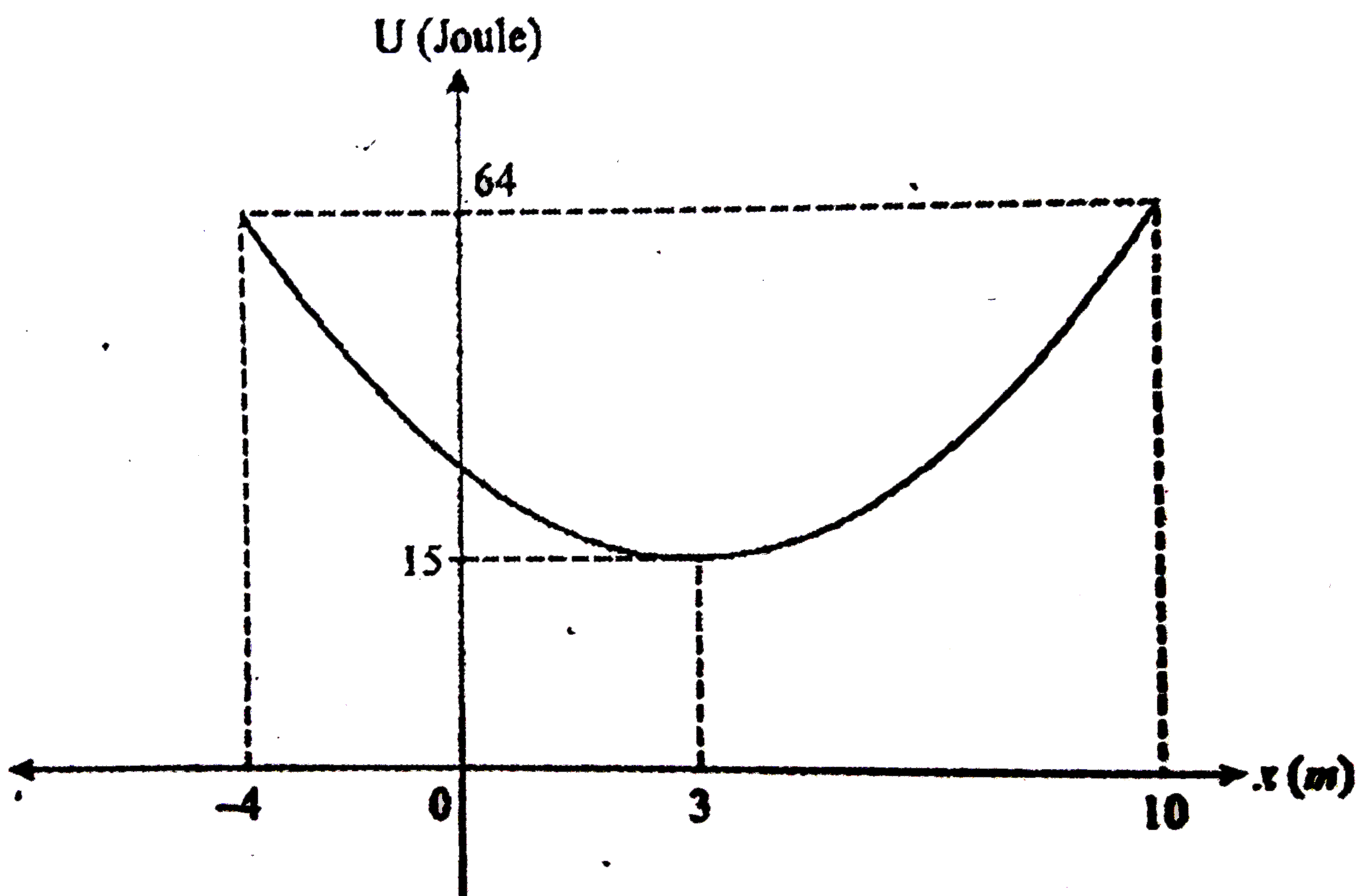
View Solutionx-अक्ष पर दोलन करते एक कण की स्थितिज ऊर्जा
U=20+(x−2)2
यहाँ U जूल में तथा x मीटर में है। कण की कुल यान्त्रिक ऊर्जा 36 जूल है
(a) दिखाओ की कण की गति सरल आवर्त है अथवा नहीं
(b) माध्य स्थिति ज्ञात कीजिए
(c )कण की अधिकतम गतिज ऊर्जा ज्ञात कीजिए
View Solutionx अक्ष के अनुदिश दोलन करने वाले कण की स्थिति ऊर्जा U−20+(x−2)2 है।
यहाँ U जूल में तथा x मीटर में है। कण की कुल यांत्रिक ऊर्जा 36 जूल है।
(a) ज्ञात कीजिए कण की गति सरल आवर्ती होगी अथवा नहीं।
(b) इसकी मध्य स्थिति ज्ञात कीजिए।
(c) कण की अधिकतम गतिज ऊर्जा ज्ञात कीजिए।
View SolutionThe potential energy of a particle of mass 2kg moving along the x-axis is given by U(x)=4x2−2x3( where U is in joules and x is in meters). The kinetic energy of the particle is maximum at
View SolutionPotential energy of a particle along x-axis varies as U = - 30 + (X−2)2, where U is in joule and x is in meter. Hence the particle is in
View SolutionThe potential energy U of a particle oscillating along x-axis is given as U=10−20x+5x2. If it is released at x=−2, then maximum value of x is
View SolutionThe potential energy of a particle oscillating along x-axis is given as
U=20+(x−2)2
Here, U is in joules and x in meters. Total mechanical energy of the particle is 36J.
(a) State whether the motion of the particle is simple harmonic or not.
(b) Find the mean position.
(c) Find the maximum kinetic energy of the particle.
View SolutionA particle moving on x - axis has potential energy U = 2 - 20x + 5x^(2) joule along x - axis. The particle is relesed at x = -3 . The maximum value of x will be ( x is in metre)
View Solution
