A block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).

The correct Answer is:6
For maximum speed,
dvdt=0⇒a=0
If at maximum speed, elongation is x, then
F=kx⇒x=Fk
Now, by WET.
−12kx2+Fx=12mv2
V=F√mk=6m/s
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Physics
Explore 775 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 2
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
Similar Questions
A block of mass m=2kg is connected to a spring of force constant k=50n/m. Initially the block is at rest and the spring has natural length . A constant force f=60N, is applied horizontally towards right, the maximum speed of the block (in m/s will be (neglect frication).

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solution
Knowledge Check

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2A block of mass 1kg is connected with a massless spring of force constant 100N/m. At t=0, a constant force F=10N is applied on the block. The spring is in its netural length at t=0. The speed of particel at x=6cm form mean position is
 A4cm/sB10cm/sC80cm/sD50cm/s
A4cm/sB10cm/sC80cm/sD50cm/sA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
A(a) MF(m+M)B(b) mFMC(c) (M+m)FmD(d) mF(m+M)
Two blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
View SolutionA block of mass 1kg is connected with massless spring of constant 100N/m .At t=0 ,a constant force F=10N is applied on the block. The spring is in its natural length at t=0.The speed of particle at x=6cm form mean position is
View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
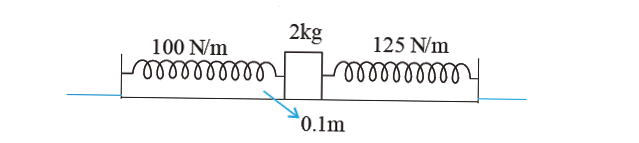
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View Solution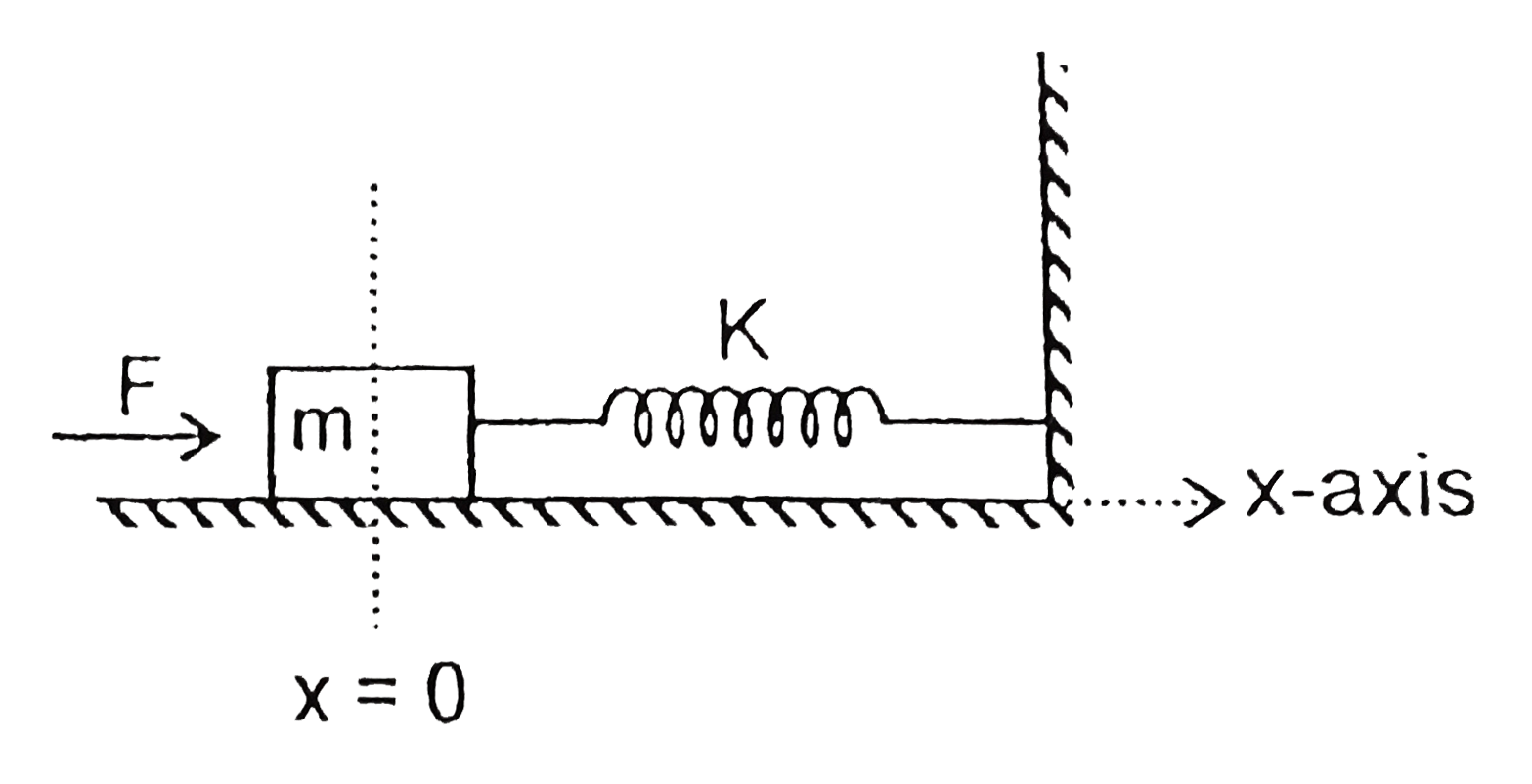
A block of mass m connected to a spring of stiffness k is placed on horizontal smooth surface. When block is at x=0, spring is in natural length. The block is also subjected to a force F=k|x|∘ then
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View Solution

