
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
mgh=12kx2
mg(h+x)=12kx2
mgh=12k(x+h)2
mg(h+x)=12k(x+h)2
The correct Answer is:B
Step by step video, text & image solution for A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A block of massm, initally at rest is dropped from a height h onto a spring whose force constant is K. Find the maximum distance x through which the spring will be compressed.
View SolutionA block of mass 2 kg initially at rest is dropped from a height of 1m into a vertical spring having force constant 490Nm−1. Calculate the maximum distance through which the spring will be compressed.
View Solution
Knowledge Check
A slab S of mass m released from a height h0, from the top of a spring of force constant k. The maximum compression x of the spring is given by the equation.
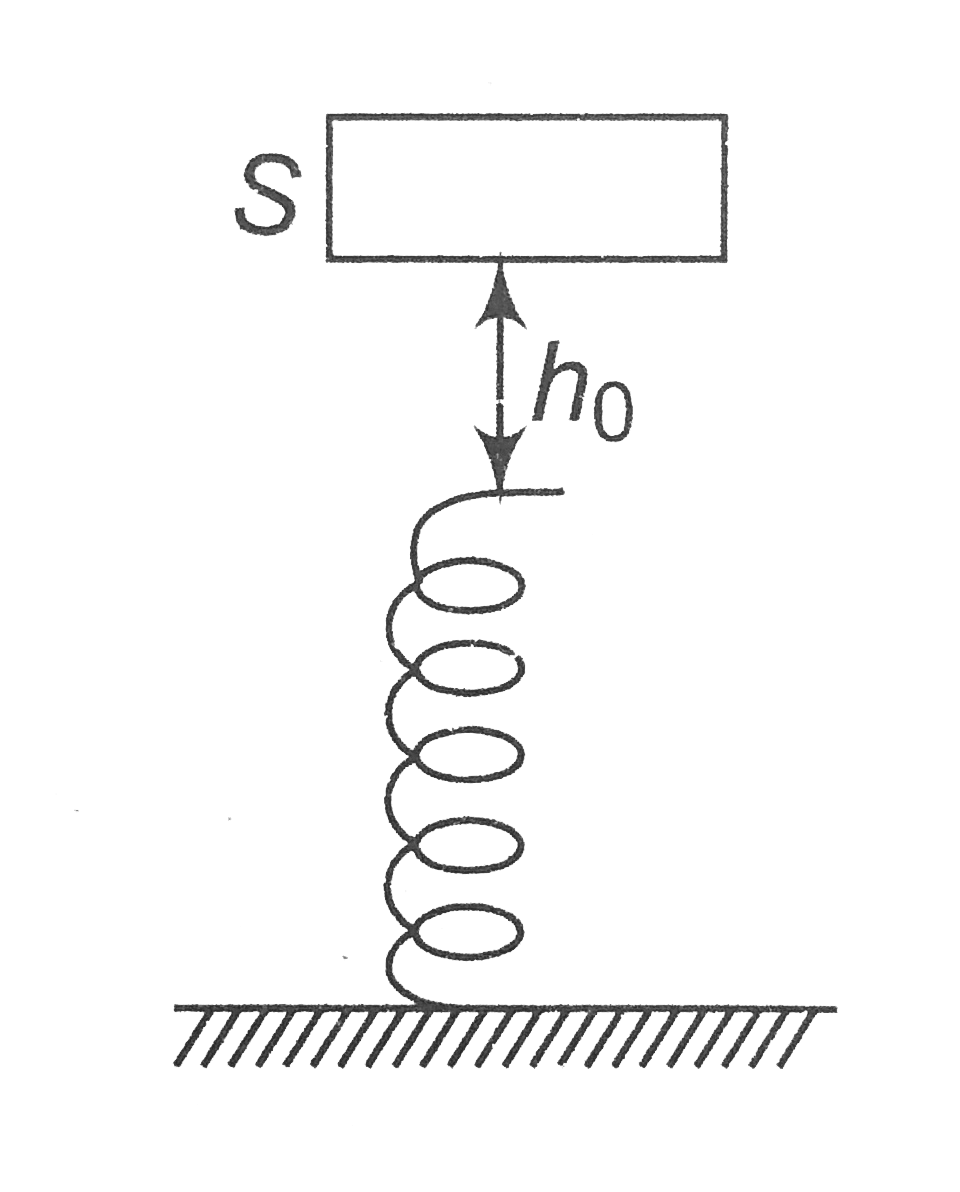 Amgh0=12kx2Bmg(h0−x)=12kx2Cmgh0=12k(h0+x)2Dmg(h0+x)=12kx2
Amgh0=12kx2Bmg(h0−x)=12kx2Cmgh0=12k(h0+x)2Dmg(h0+x)=12kx2A ball of mass m moving with speed v0 strikes a block of mass 3m kept at rest. The collision is completely inelastic . If k is spring constant , the maximum compression of the spring is
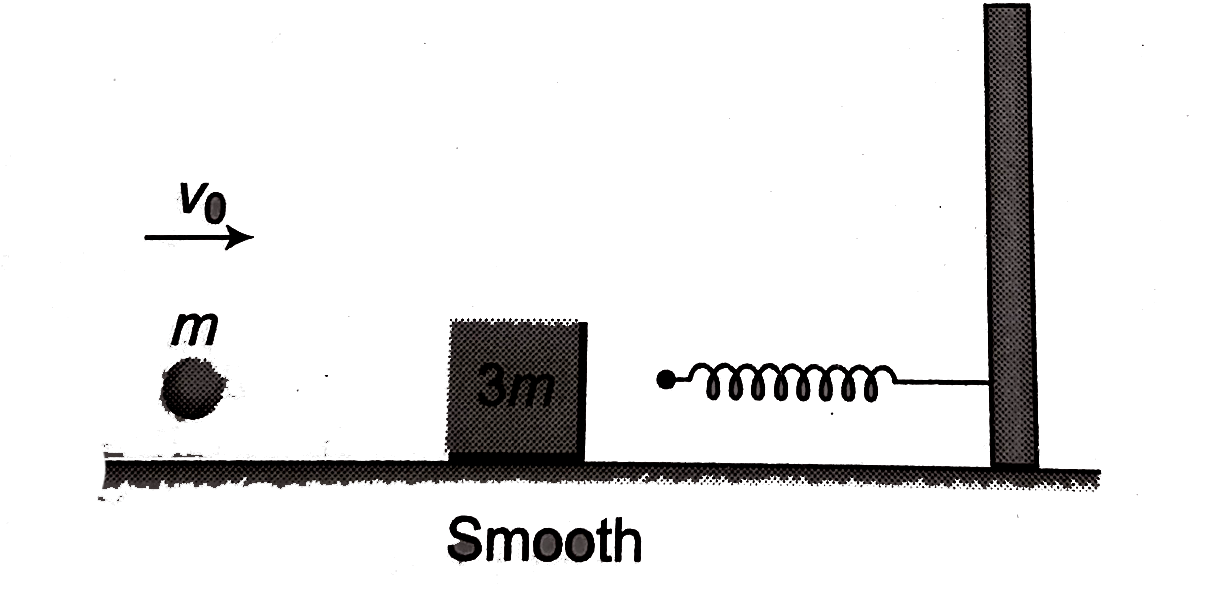 A√mv20kB√mv202kC√mv203kD√mv204k
A√mv20kB√mv202kC√mv203kD√mv204kA block of mass 2kg is propped from a height of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5cmB15cmC26cmD10cm
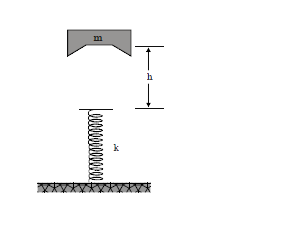
A smooth block of mass m is released from rest from a height h. It slides and compresses the spring of stiffness k. Find the maximum compression of the spring .
Taking block spring a system. Now external force is doing work on system and no non-conservative force is present. The mechanincal energy should be conserved.
ΔK+ΔU=0
View SolutionA block of mass m = 2.0 kg is dropped from height h = 40 cm onto a spring of spring constant k=1960N/s. Find the maximum distance through which the spring is compressed. Take g=9.8m/s2
View SolutionA 2-kg block is dropped from a height of 0.4 m on a spring of force constant k=1960N. Find the maximum distance the spring will be compressed. (Take g=9.8ms−2)
[Hint : Consider conservation of energy]
View SolutionTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
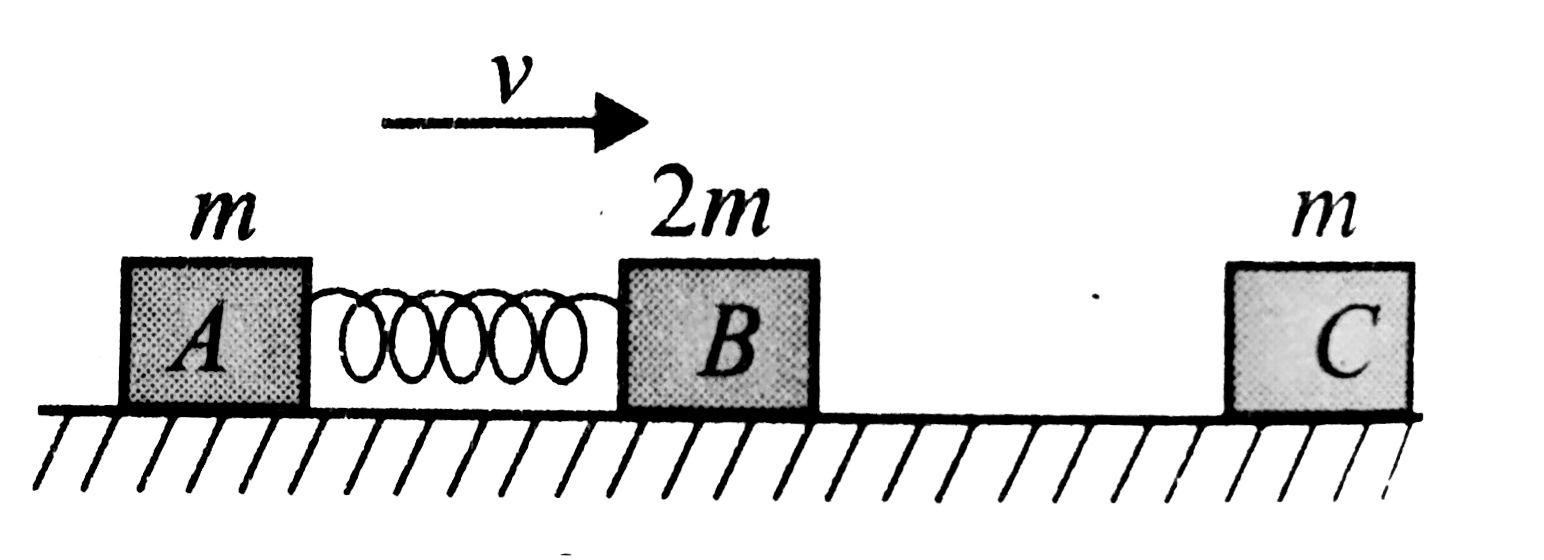
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View Solution

