A 2-kg block is dropped from a height of 0.4 m on a spring of force constant . Find the maximum distance the spring will be compressed. (Take )
[Hint : Consider conservation of energy]
The correct Answer is:0.1 m
To solve the problem of finding the maximum distance the spring will be compressed when a 2-kg block is dropped from a height of 0.4 m onto a spring with a force constant k=1960N/m, we can use the principle of conservation of energy.
1. Identify the energies involved:
- The block has gravitational potential energy when it is at height h=0.4m.
- When the block compresses the spring, this potential energy is converted into the elastic potential energy of the spring.
2. Calculate the gravitational potential energy (PE):
PE=mgh
where:
- m=2kg
- g=9.8m/s2
- h=0.4m
Substituting the values:
PE=2×9.8×0.4=7.84J
3. Set up the equation for elastic potential energy (EPE):
The elastic potential energy stored in the spring when it is compressed by a distance x is given by:
EPE=12kx2
where k=1960N/m.
4. Apply conservation of energy:
At the maximum compression of the spring, all the gravitational potential energy will be converted into elastic potential energy:
mgh=12kx2
Substituting the known values:
7.84=12×1960×x2
5. Solve for x2:
Rearranging the equation gives:
7.84=980x2
x2=7.84980
x2=0.008
6. Calculate x:
Taking the square root of both sides:
x=√0.008=0.0894m
7. Final answer:
The maximum distance the spring will be compressed is approximately 0.0894m or 8.94cm.
- The block has gravitational potential energy when it is at height h=0.4m.
- When the block compresses the spring, this potential energy is converted into the elastic potential energy of the spring.
PE=mgh
where:
- m=2kg
- g=9.8m/s2
- h=0.4m
PE=2×9.8×0.4=7.84J
The elastic potential energy stored in the spring when it is compressed by a distance x is given by:
EPE=12kx2
where k=1960N/m.
At the maximum compression of the spring, all the gravitational potential energy will be converted into elastic potential energy:
mgh=12kx2
Substituting the known values:
7.84=12×1960×x2
Rearranging the equation gives:
7.84=980x2
x2=7.84980
x2=0.008
Taking the square root of both sides:
x=√0.008=0.0894m
The maximum distance the spring will be compressed is approximately 0.0894m or 8.94cm.
Topper's Solved these Questions
- FRICTION, WORK POWER AND ENERGYBOOK - NN GHOSHCHAPTER - FRICTION, WORK POWER AND ENERGYEXERCISE - Exercises (B)
36 Videos
- FRICTION, WORK POWER AND ENERGYBOOK - NN GHOSHCHAPTER - FRICTION, WORK POWER AND ENERGYEXERCISE - Exercises (B)
36 Videos
- FIRST LAW OF THERMODYNAMICSBOOK - NN GHOSHCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - All Questions
39 Videos
- GRAVITATIONBOOK - NN GHOSHCHAPTER - GRAVITATIONEXERCISE - EXERCISE
29 Videos
Similar Questions
A block of mass m = 2.0 kg is dropped from height h = 40 cm onto a spring of spring constant k=1960N/s. Find the maximum distance through which the spring is compressed. Take g=9.8m/s2
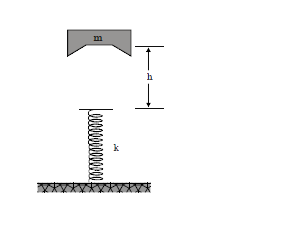
View SolutionA block of massm, initally at rest is dropped from a height h onto a spring whose force constant is K. Find the maximum distance x through which the spring will be compressed.
View Solution
Knowledge Check
A block of mass 2kg is propped from a height of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5cmB15cmC26cmD10cm
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2A slab S of mass m released from a height h0, from the top of a spring of force constant k. The maximum compression x of the spring is given by the equation.
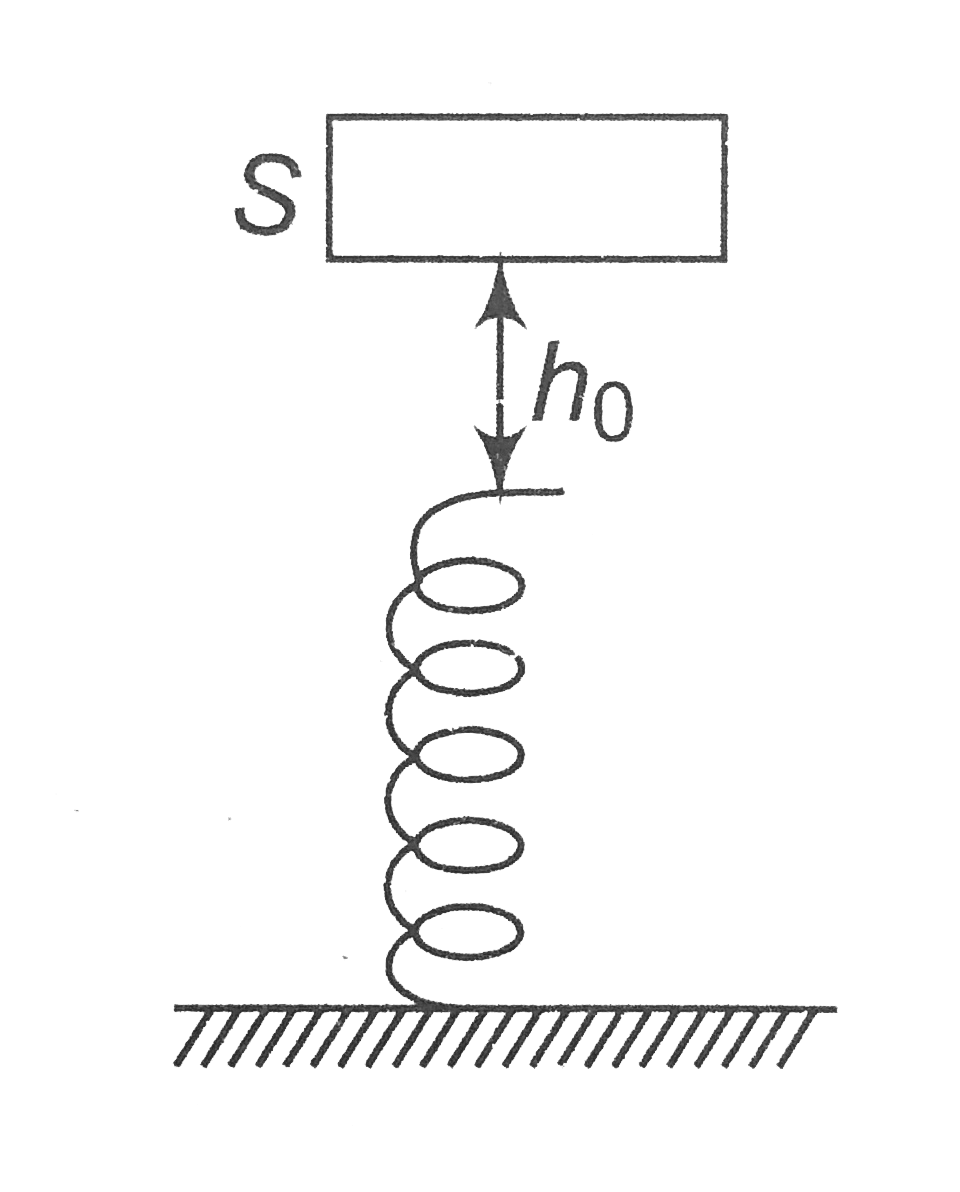 Amgh0=12kx2Bmg(h0−x)=12kx2Cmgh0=12k(h0+x)2Dmg(h0+x)=12kx2
Amgh0=12kx2Bmg(h0−x)=12kx2Cmgh0=12k(h0+x)2Dmg(h0+x)=12kx2
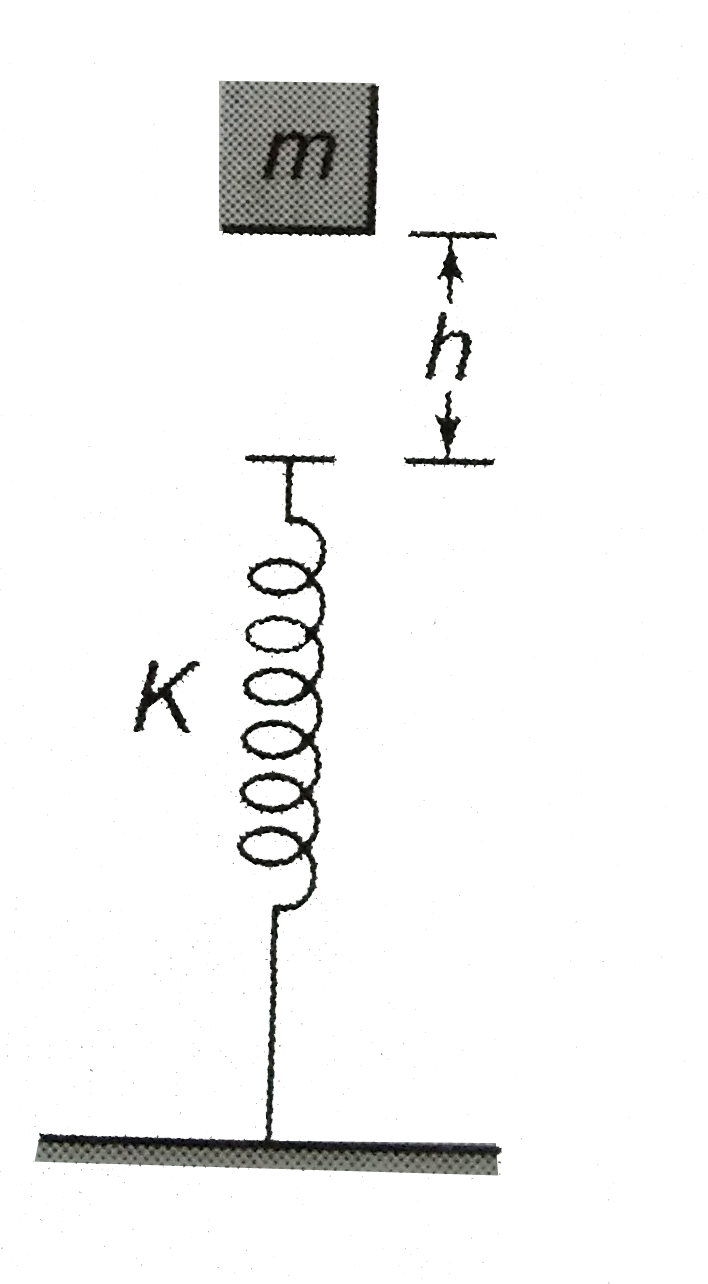
A block is released from height h, find the maximum compression of spring of spring constant k.
View SolutionA block of mass 2 kg initially at rest is dropped from a height of 1m into a vertical spring having force constant 490Nm−1. Calculate the maximum distance through which the spring will be compressed.
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View Solution
