A particle starts from point A, moves along a straight line path with an accleration given by a=2(4−x) where x is distance from point A. The particle stops at point B for a moment. Find the distance AB (in m). (All values are in S.I. units)
The correct Answer is:8
vdvdx=8−2x
⇒v∫0vdv=x∫0(8−2x)dx⇒v22=8x−x2
⇒v2=16x−2x2
At B,v=0 so, x=8
Hence, AB=8
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Physics
Explore 775 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 2
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
Similar Questions
A particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q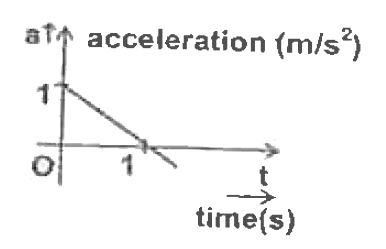
View SolutionA particle starts moving in a straight line from rest with an acceleration (inm/s2) given by : a=12√x, where x is the distance travelled by the particle (in meters ) The velocity of the particle at the instant when its acceleration is 48m/s2 is .......m/s
View Solution
Knowledge Check
A particle starts from point A moves along a straight line path with an acceleration given by a=p−qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qpThe speed v of a particle moving along a straight line is given by a+bv2=x2 (where x is its distance from the origin). The acceleration of the particle is
AbxBx/aCx/bDx/abThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
AxbBxabCabxDax
A particle starts from rest and moves along a straight line with uniform acceleration. The ratio of distance travelled by the particle during the first three seconds to the distance travelled by the particle during the next three seconds is 3 о 2
View SolutionA particle starts from rest and moves along a straight line with uniform acceleration. The ratio of distance travelled by the particle during the first three seconds to the distance travelled by the particle during the next three seconds is 3 о 2
View SolutionA particle moves in a straight line in such a way that its velocity at any point is given by v2=2−3x, where x is measured from a fixed point. The acceleration is
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2, where x is its distance from the origin. The acceleration of the particle is
View Solutiona particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View Solution

