
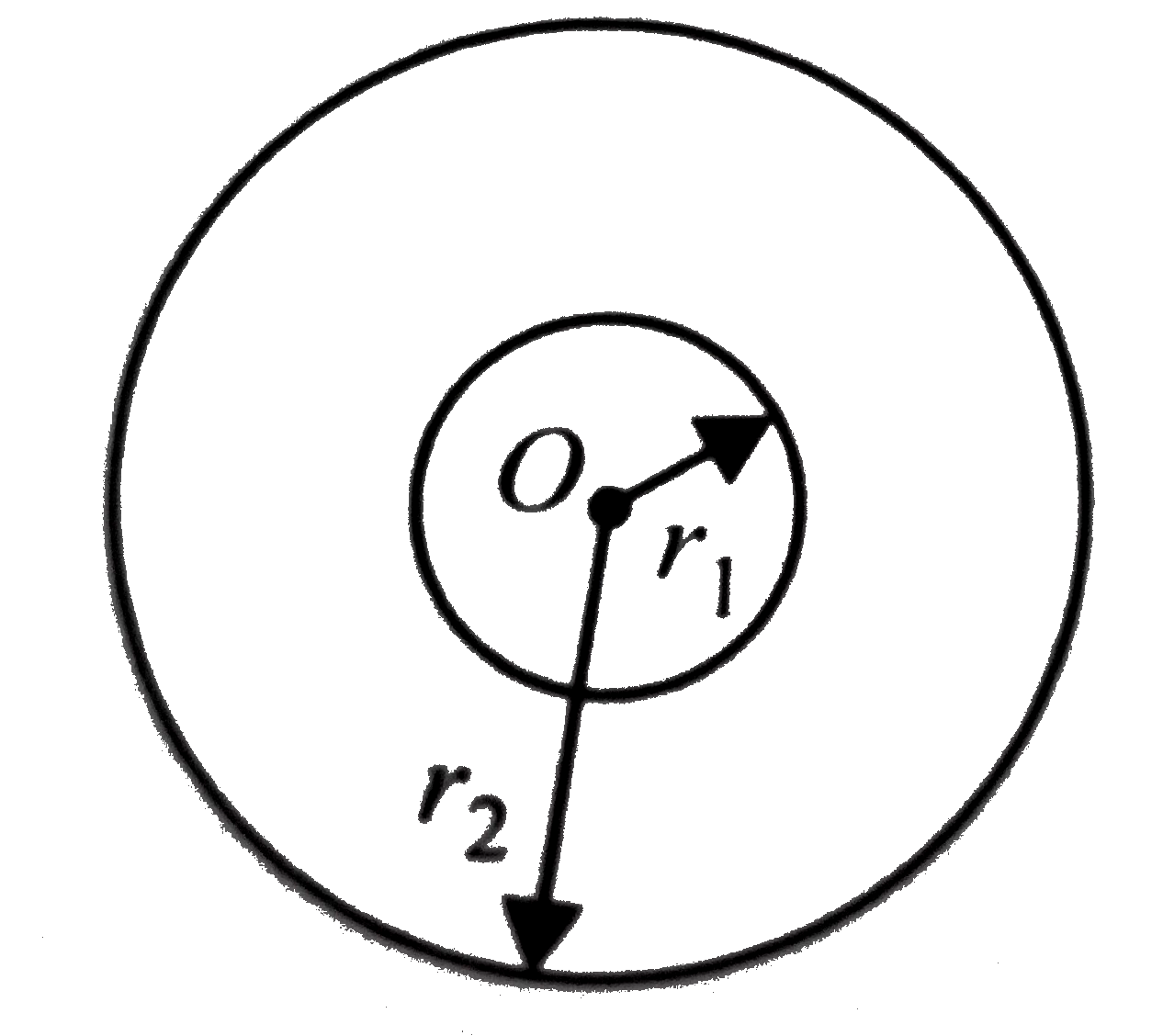
There are two concentric cylinders of radii and as shown. The narrow space between the two cylinders is filled with liquid of viscosity . The inner cylinder is held stationary by means of a torsional spring of stiffness G. the outer cylinder is rotated with constant angular speed . The torque acting on the inner cylinder due to shearing action of thhe liquid:
The correct Answer is:A
The torque due to liquid in annular space is
where velocity gradient
Also torque due to liquid in between space in botto of thickness 'h'
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A cylinder of mass M, radius r1 and lenglth l is kept inside another cylinder of radius r2 and length l. The space between them is filled with a liquid of viscosity η. The inner cylinder starts rotating with angular velocity ω while the other cylinder is at rest. Find time when inner cylinder stops.
View SolutionA gas fills up the space between two long coaxial cylinders of radii R1 and R2, with R1<R2. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. The moment of friction forces acting on a unit length of the inner cylinder is equal to N1. Find the viscosity coefficient η of the gas taking into account that the friction force acting on a unit area of the cylindrical surface of radius r is determined by the formule σ=ηr(∂ω/∂r).
View Solution
Knowledge Check
Space between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
 Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.A long, hollow insulating cylinder of radius R and negligible thickness has a uniform surface charge density σ. The cylinder rotates about its central axis at a constant angular speed ω. Choose the correct option(s):
AThe charge crossing an imaginary line of length L on the surface of the cylinder, parallel to its axis, per unit time, is ωσRL.BThe magnetic moment of a length L of the cylinder is πωσR3LCThe magnetic field intensity at a point on the axis of the cylinder, inside the cylinder, is μ0ωσR2DIf the direction of rotation of the cylinder is reversed, the magnetic field at a point on the axis of the cylinder will also reverse direction
A fluid with viscosity η fills the space between two long co-axial cylinders of radii R1and R2, with R1<R2. The inner cylinder is stationary while the outer one is rotated with a constant angular velocity ω2. The fluid flow is laminar. Taking into account that the friction force acting on a unit area of a cylindrical surface of radius r is defined by the formula σ=ηr(∂ω/∂r), find:
(a) the angular velocity of the rotating fluid is as a function of radius r,
(b) the moment of the friction forces acting on a unit length of the outer cylinder.
View SolutionThere are two co-axial non conducting cylinders of radii a and b(>a). Length of each cylinder is L(>>b) and their curved surfaces have uniform surface charge densities of–σ (on cylinder of radius a) and +σ (on cylinder of radius b). The two cylinders are made to rotate with same angular velocity ω as shown in the figure. The charge distribution does not change due to rotation. Find the electric field (E) and magnetic field (B) at a point (P) which is at a distance r from the axis such that (a) 0<r<a (b) a<r<b (c) r>b. Assume that point P is close to perpendicular bisector of the length of the cylinders

View SolutionFind the temperature distribution in the space between two coaxial cylinders of radii R1 and R2 filled with a uniform heat conducting substance if the temperatures of the cylinders are constant and are equal to T1 and T2 respectively.
View SolutionUnder standard conditions helium fills up the space between two long coaxial cylinders. The mean radius of the cylinders is equal to R, the gap between them is equal to ΔR, with ΔR<<R. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. Down to what magnitude should the helium pressure be lowered (keeping the temperature constant) to decrease the sought moment of friction forces n=10 times if ΔR=6mm ?
View SolutionTwo cylinders having radiii R1 and R2 and rotational inertia I1 and I2 respectively, are supported by fixed axes perpendicular to the plane of figure-5.52. The large cylinder is initially rotating with angular velocityω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually, slipping ceases, and the two cylinders rotate at constant rates in opposite directions, (a) Find the final angular velocity ω2 of the small cylinder in terms of I1,I2,R1,R2 and ω0. (b) Is total angular momentum conserved in this case ?
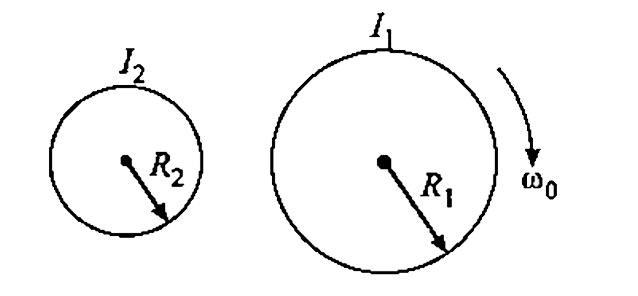
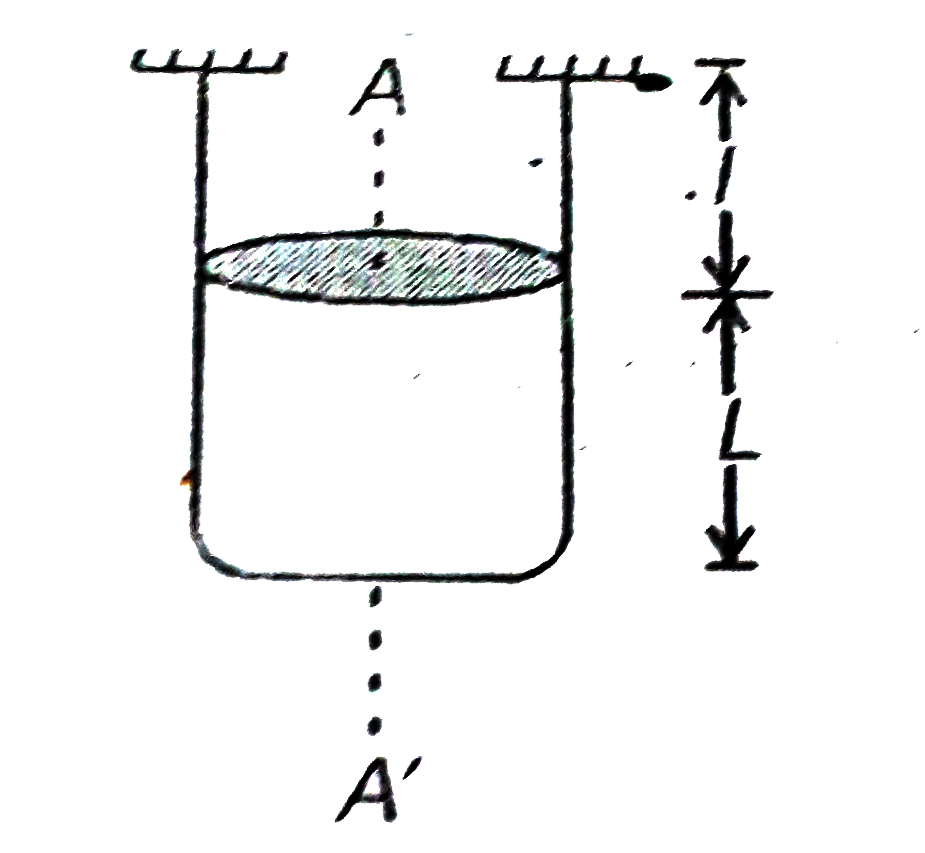
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
View Solution
