A long, hollow insulating cylinder of radius R and negligible thickness has a uniform surface charge density σ. The cylinder rotates about its central axis at a constant angular speed ω. Choose the correct option(s):
The charge crossing an imaginary line of length L on the surface of the cylinder, parallel to its axis, per unit time, is ωσRL.
The magnetic moment of a length L of the cylinder is πωσR3L
The magnetic field intensity at a point on the axis of the cylinder, inside the cylinder, is μ0ωσR2
If the direction of rotation of the cylinder is reversed, the magnetic field at a point on the axis of the cylinder will also reverse direction
The correct Answer is:A, B, D
To solve the problem regarding the long hollow insulating cylinder with a uniform surface charge density that rotates about its central axis, we will analyze the situation step by step.
Step 1: Understanding the System
We have a long hollow insulating cylinder of radius R with a uniform surface charge density σ. The cylinder rotates about its central axis at a constant angular speed ω.
Step 2: Charge Crossing an Imaginary Line
To find the charge crossing an imaginary line of length L on the surface of the cylinder per unit time, we can use the following reasoning:
1. The total charge dq on the surface of the cylinder can be expressed as:
dq=σ⋅dA
where dA is the area element.
2. The area of the cylindrical surface for a length L is given by:
dA=2πR⋅L
3. The total charge Q on the surface of length L is:
Q=σ⋅2πR⋅L
4. The time period T of one complete rotation is:
T=2πω
5. The charge crossing the imaginary line per unit time is:
Charge per unit time=QT=σ⋅2πR⋅L2πω=σ⋅ω⋅R⋅L
Step 3: Magnetic Moment Calculation
Next, we need to find the magnetic moment M of the cylinder:
1. The magnetic moment M is given by:
M=I⋅A
where I is the current and A is the area.
2. The current I can be expressed as:
I=dqdt
where dq=σ⋅dA.
3. The area A for the circular cross-section of the cylinder is:
A=πR2
4. Substituting I:
I=σ⋅ω⋅R⋅L
5. Therefore, the magnetic moment M becomes:
M=I⋅A=(σ⋅ω⋅R⋅L)⋅πR2=πσωR3L
Step 4: Magnetic Field Intensity Calculation
Now, we need to find the magnetic field intensity B at a point on the axis of the cylinder:
1. The magnetic field intensity B at a distance x from the center of the cylinder can be calculated using the formula:
B=μ0I2R2+x2⋅R22
2. Integrating over the entire length of the cylinder gives:
B=μ0σωR32∫dx(R2+x2)3/2
3. The limits of integration are from −∞ to +∞, leading to:
B=μ0σωR
Step 5: Effect of Reversing Rotation
If the direction of rotation of the cylinder is reversed, the magnetic field direction will also reverse. This is due to the right-hand rule applied to the direction of current and the resulting magnetic field.
Conclusion
The correct options based on the calculations are:
1. The charge crossing an imaginary line of length L is σωRL.
2. The magnetic moment is πσωR3L.
3. The magnetic field intensity at a point on the axis is μ0σωR.
4. Reversing the cylinder's rotation reverses the magnetic field direction.
We have a long hollow insulating cylinder of radius R with a uniform surface charge density σ. The cylinder rotates about its central axis at a constant angular speed ω.
To find the charge crossing an imaginary line of length L on the surface of the cylinder per unit time, we can use the following reasoning:
dq=σ⋅dA
where dA is the area element.
dA=2πR⋅L
Q=σ⋅2πR⋅L
T=2πω
Charge per unit time=QT=σ⋅2πR⋅L2πω=σ⋅ω⋅R⋅L
Next, we need to find the magnetic moment M of the cylinder:
M=I⋅A
where I is the current and A is the area.
I=dqdt
where dq=σ⋅dA.
A=πR2
I=σ⋅ω⋅R⋅L
M=I⋅A=(σ⋅ω⋅R⋅L)⋅πR2=πσωR3L
Now, we need to find the magnetic field intensity B at a point on the axis of the cylinder:
B=μ0I2R2+x2⋅R22
B=μ0σωR32∫dx(R2+x2)3/2
B=μ0σωR
If the direction of rotation of the cylinder is reversed, the magnetic field direction will also reverse. This is due to the right-hand rule applied to the direction of current and the resulting magnetic field.
The correct options based on the calculations are:
1. The charge crossing an imaginary line of length L is σωRL.
2. The magnetic moment is πσωR3L.
3. The magnetic field intensity at a point on the axis is μ0σωR.
4. Reversing the cylinder's rotation reverses the magnetic field direction.
Similar Questions
An infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View SolutionRepeat the question if sphere is a hollow non-conducting sphere of radius R and has uniform surface charge density σ.
View Solution
Knowledge Check
A thin annular disc of outer radius R and R2 inner radius has charge Q uniformly distributed over its surface. The disc rotates about its axis with a constant angular velocity ω. Choose the correct option(s):
AThe magnetic field intensity at the centre of the disc is μ0Qω3πRBThe magnetic field intensity at the centre of the disc is μ0Qω4RCThe magnetic moment of the disc is 5QωR216DThe magnetic moment of the disc is 3QωR24A circular cylinder of radius R and height H is filled with water to a height (2/3)H. It starts rotating about its axis with constantly increasing angular speed. Choose the correct alternatives.
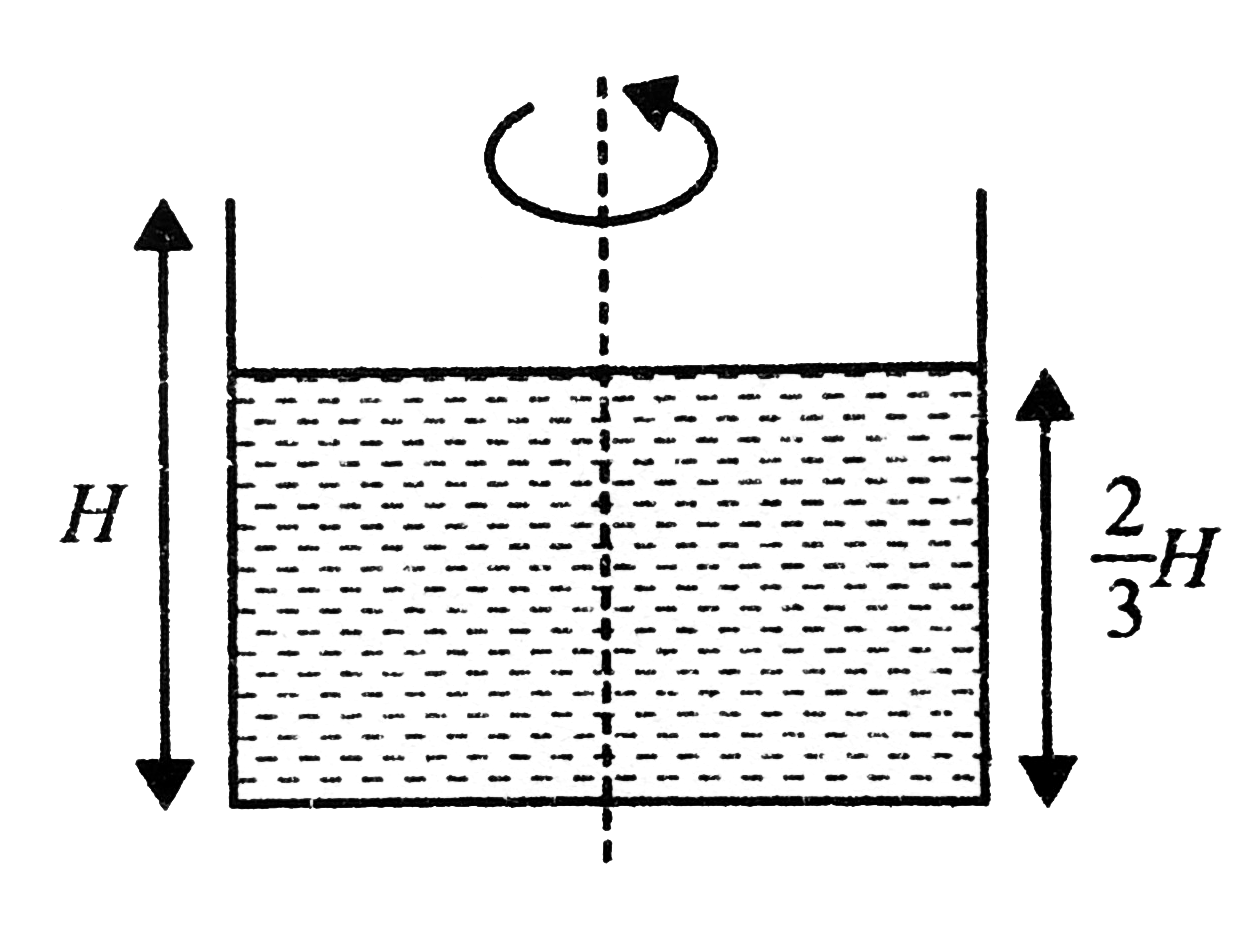 AAt all speeds, shape of the free surface is parabolloid.BThe free surface touches first the brim of the cylinder and then the base of the cylinder.CThe free surface cannot touch the base without spilling water.DThe free surface touches the brim as well as the base at the same instant.
AAt all speeds, shape of the free surface is parabolloid.BThe free surface touches first the brim of the cylinder and then the base of the cylinder.CThe free surface cannot touch the base without spilling water.DThe free surface touches the brim as well as the base at the same instant.A thin circular disk of radius R is uniformly charged with density σ>0 per unit area.The disk rotates about its axis with a uniform angular speed ω.The magnetic moment of the disk is :
AπR4σωBπR42σωCπR44σωD2πR4σω
A flat disc of radius R charged uniformly on its surface at a surface charge density σ. About its central axis of rotation it rotates at an angular speed ω. Find the magnetic moment of disc due to rotation of charges.
View SolutionA flat insulating disc of radius 'a' carries an excess charge on its surface is of surface charge density σC/m2. Consider disc to rotate around the perpendicular to its plane with angular speed ωrad/s/ If magnetic field →B is directed perpendicular to the roation axis, then find the torque acting on the disc.
View SolutionA flat dielectric disc of radius R carries an exces charge on its surface. The surface charge density σ. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity ω. Find the toruque on the disc if it is placed in a uniform magnetic field B directed perpendicular to the rotation axis.
View SolutionA particle is revolving in a circle of radius r and centre at 'O' with uniform angular velocity ω. Choose the correct option(s) :

View SolutionA very long metallic hollow pipe of length l and radius r(<<l) is carrying charge Q , uniformly distributed upon it . The pipe is rotated about its axis with constant angular speed ω . The energy stored in the pipe of length l100 is
View Solution
