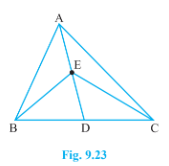
In a ABC,E is the mid-point of median AD. Show that ar(BED)=14ar(ABC)
Since AD is the median of △ABC.
∴ar(△ABD=(△ADC)
ar(△ABD)=12ar(△ABC)......(1)
In △ABD,
BE is the median,
ar(△BED)=ar(△BAE)
ar(△BED)=12ar(ABD)
ar(△BED)=12×12ar(△ABC)
From eq (1)
=ar(△BED)=14ar(△ABC)
Hence proved.
Topper's Solved these Questions
Similar Questions
In a ABC,E is the mid-point of median AD. Show that ar(BED)=14ar(ABC)
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE, prove that ar ( BOE)=18ar ( ABC)
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=14ar(ABC)
View SolutionIn ABC, E is the mid-point of median AD such that BE produced meets AC at F. If AC=10.5 CM, then AF= 3cm (b) 3.5cm (c) 2.5cm (d) 5cm
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionAny point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
View SolutionIn Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).
View Solution