In Fig.9.23, E is any point on median AD of a . Show that
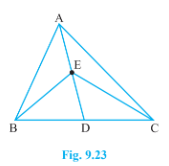
We know that the median divides a triangle into two triangles of equal areas. is the median for and is the median of
Since is the median of . Therefore, it will divide into two triangles of equal areas.
Hence, ... (1)
Similarly, is the median of .
Hence, ... (2)
Substract equation (2) from equation (1), we obtain
Similar Questions
In Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).

View SolutionIn the figure, E is any point on median AD of a △ABC. Show that ar(△ABE)= ar(△ACE).
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View SolutionIn Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
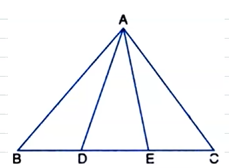
View SolutionD and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(ADEG)=ar(GBCE)
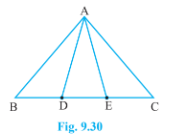
View SolutionIn Fig. 9.30, D and E are two points on BC such that BD = DE = EC. Show thatar (ABD) = ar (ADE) = ar (AEC). Can you now answer the question that you have left in the Introduction of this chapter, whether the field of Budha has been actually divided into three parts of equal area ?
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn Fig. 4.124, E is a point on side CB produced of an isosceles triangle ABC with AB=AC . If AD⊥BC and EF⊥AC , prove that (i) ABDECF (ii) AB×EF=AD×EC . (FIGURE)
View SolutionAny point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
View Solution
