In Fig. 9.30, D and E are two points on BC such that BD = DE = EC. Show thatar (ABD) = ar (ADE) = ar (AEC). Can you now answer the question that you have left in the Introduction of this chapter, whether the field of Budha has been actually divided into three parts of equal area ?
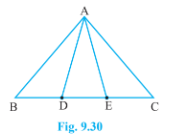
Let's draw an altitude that will help us to find areas of all three triangles. Let us draw AL⊥BC.
We know that,Areaofa△ = 12× Base × Altitude
Area(△ADE)=12×DE×AL
Area(△ABD)=12×BD×AL
Area(△AEC)=12×EC×AL
DE=BD=EC (Given)
Thus, 12×DE×AL=12×BD×AL=12×EC×AL
Therefore, ar(△ADE)=ar(△ABD)=ar(△AEC)
Yes, we can now say that the field of Budhia has been actually divided into three parts of equal area.
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 9.1
1 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise 9.2
6 Videos
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - EXERCISE 10.2
2 Videos
Similar Questions
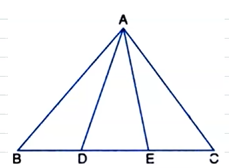
In Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
View SolutionIn Figure, ABCDandAEFD are two parallelograms? Prove that: ar(APE):ar(PFA)=ar(QFD):ar(PFD)
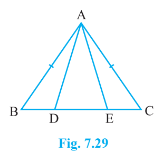
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View SolutionIn Fig. 4.101, AD and CE are two altitudes of ABC . Prove that AEF~CDF (ii) ABD~CBE (iii) AEF~ADB (iv) FDC~BEC (FIGURE)
View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
View SolutionD and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar (ACB)=ar (ACF) ar (AEDF)=ar (ABCDE)
View SolutionIn a ABC , D and E are points on AB and AC respectively such that DE/BC . If AD=2.4cm, AE=3.2cm, DE=2cm and BC=5cm , find BD and CE .
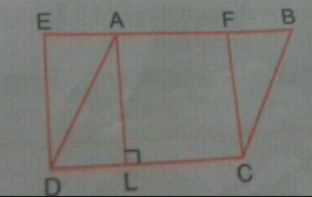
View SolutionIn the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.
View Solution
