AD is one of the medians of a ABC..X is any point on AD . Show that ar(ABX)=ar(ACX)
Video Solution
Text Solution
Solution:
△ABC,
AD is median,
ar(△ABD)=ar(△ADC)......(1)
△XBC,
XD is median,
ar(XBD)=ar(XDC)......(2)
Substract eq (2) from (1)
ar(△ABD)−ar(△XBD)=ar(△ADC)−ar(△XDC)
ar(△ABX)=ar(△ACX)
Hence proved.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, AD is the median and E is any point on AC, such that ar(ΔMDE) : ar(ΔABD) = 2 : 3, then find the ratio of ar(ΔEDC): ar(ΔABC).
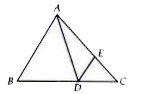 A3 : 4B1 : 6C6 : 1D4 : 3
A3 : 4B1 : 6C6 : 1D4 : 3
In a ABC,E is the mid-point of median AD. Show that ar(BED)=14ar(ABC)
View SolutionIn Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).
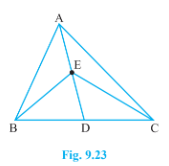
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
View SolutionIn the figure, E is any point on median AD of a △ABC. Show that ar(△ABE)= ar(△ACE).
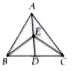
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View SolutionIn Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar(PQRS)=ar(ABRS)(ii) ar(AXS) =12ar(PQRS)

View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

View Solution

