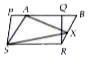
In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar(PQRS)=ar(ABRS)(ii) ar(AXS) =12ar(PQRS)

If a triangle and a parallelogram are on the same base and between the same parallel lines, the area of the triangle will be half of that of a parallelogram or if two parallelograms are on the same and between two parallel lines then their area will be equal.
i) It can be observed from the figure that parallelogram PQRS and ABRS lie on the same base SR and also, they lie between the same parallel lines SR and PB.
According to Theorem 9.1, Parallelograms on the same base and between the same parallel lines are equal in area.
Area(PQRS)=Area(ABRS) .....(1)
ii) Consider △AXS and parallelogram ABRS
As both lie on the same base AS as well as between the same parallel lines AS and BR,
Area(△AXS)=12Area(ABRS).....(2)
From Equations (1) and (2),
we obtain Area(△AXS)=12Area(PQRS)
Similar Questions
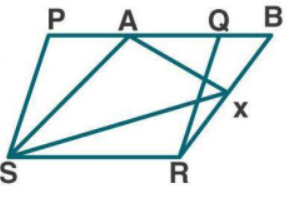
In the figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
ar(PQRS) = ar(ABRS)
View SolutionIn Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar(PQRS)=ar(ABRS)(ii) ar(AXS) =12ar(PQRS)

View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
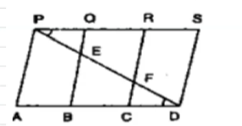
View SolutionIn Figure, PSDA is a parallelogram in which PQ=QR=RS and APBQCR. Prove that ar ( PQE)= ar ( CFD).
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).

View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
View SolutionPQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
(i) SR ∣∣ ACand SR=12AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
View SolutionIn Figure, PQRS is a parallelogram. If XandY are mid-points of PQandSR respectively and diagonal SQ is jointed. The ratio ar(| |(gm)XQRY):ar(QSR)=
(a) 1:4
(b) 2:1
(c) 1:2
(d) 1:1
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View Solution
