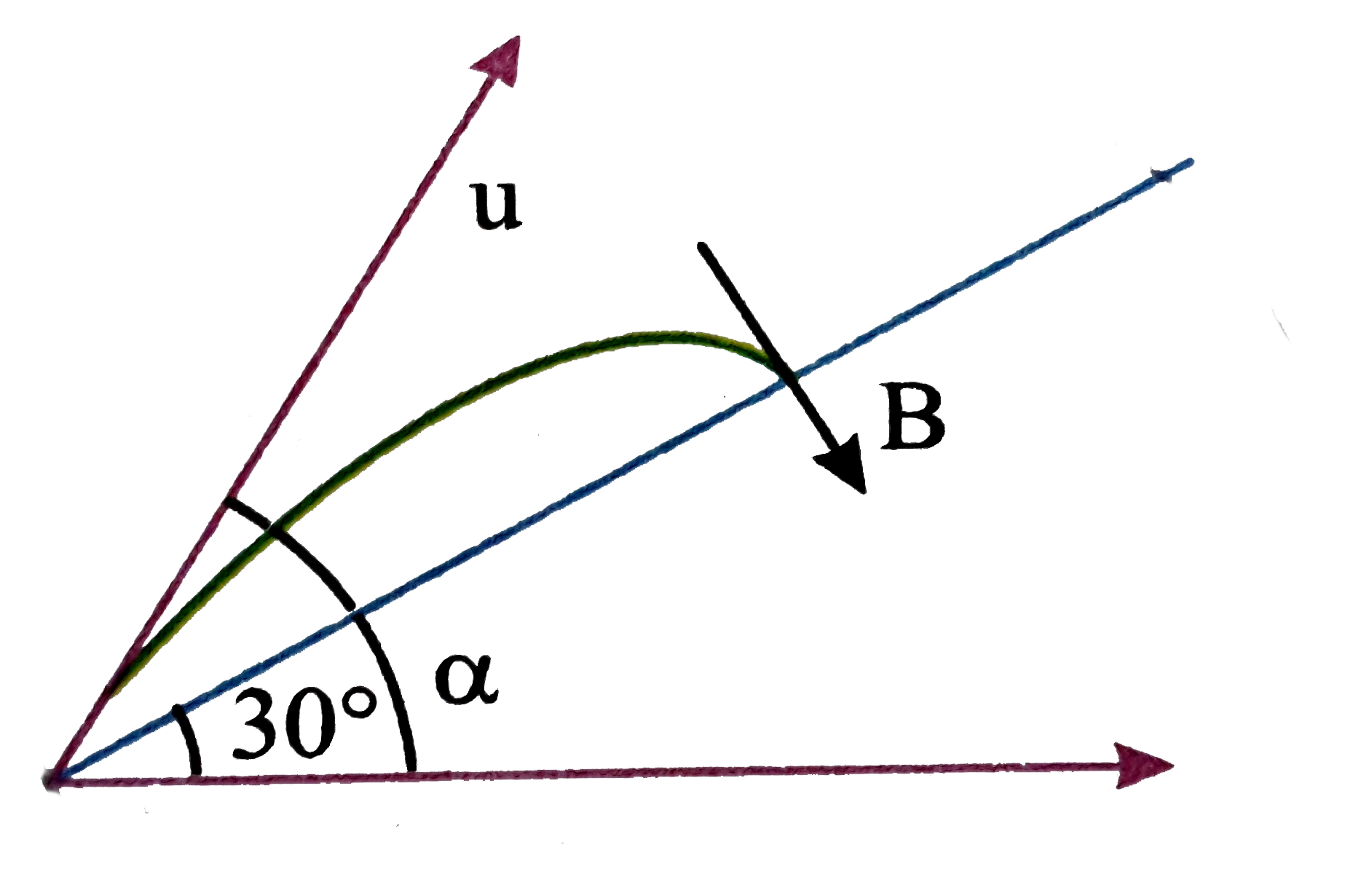
A particle is projected with a certain velocity at an angle $\propto$ above the horizontal from the foot of an inclined plane of inclination $30^{\circ}$ . If the particle strikes the plane normally, then $\propto$ is equal to.

A

$30^{\circ} + {tan}^{- 1} (\frac{1}{2 \sqrt{3}})$

B

$30^{\circ} + {tan}^{- 1} (\frac{\sqrt{3}}{2})$

C

$60^{\circ}$

D

$30^{\circ} + {tan}^{- 1} (2 \sqrt{3})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$t_{A B} =$ time of flight of the projectile
$\frac{2 u sin (α - 30^{\circ})}{g {cos 30}^{2}}$
Now component of velocity along the plane becomes zero at point $B$ .
$∴ 0 = u cos (α - 30^{\circ}) - (g {sin 30}^{2}) T$
or $u cos (α - 30^{\circ}) = (g {sin 30}^{2}) \frac{2 u sin (α - 30^{\circ})}{g {cos 30}^{\circ}}$
or $tan (α - 30^{\circ}) = \frac{1}{2 {tan 30}^{\circ}} = \frac{\sqrt{3}}{2}$
$∴ α = 30^{\circ} + {tan}^{- 1} (\frac{\sqrt{3}}{2})$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is projected with a certain velocity at an angle $α$ above the horizontal from the foot of an inclined plane of inclination $30^{\circ}$ . If the particle strikes the plane normally then $α$ is equal to
A $30^{\circ} + {tan}^{- 1} (\frac{\sqrt{3}}{2})$
B $45^{\circ}$
C $60^{\circ}$
D $30^{\circ} + {tan}^{- 1} (2 \sqrt{3})$
Question 2 - Select One
A projectile is projected with speed u at an angle of $60^{\circ}$ with horizontal from the foot of an inclined plane. If the projectile hits the inclined plane horizontally, the range on inclined plane will be.
A $\frac{u^{2} (\sqrt{21})}{2 g}$
B $\frac{3 u^{2}}{4 g}$
C $\frac{u^{2}}{2 β}$
D $\frac{(\sqrt{21}) u^{2}}{8 g}$
Question 3 - Select One
A particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is $β$ . It strikes. the plane at right angles if
A $tan (α - β) = cot β$
B $2 tan (α - β) = cot β$
C $2 cot (α - β) = cot β$
DNone of these

NARAYNA-MOTION IN A PLANE-Level -V Single answer

Home
Ask Doubt
Profile