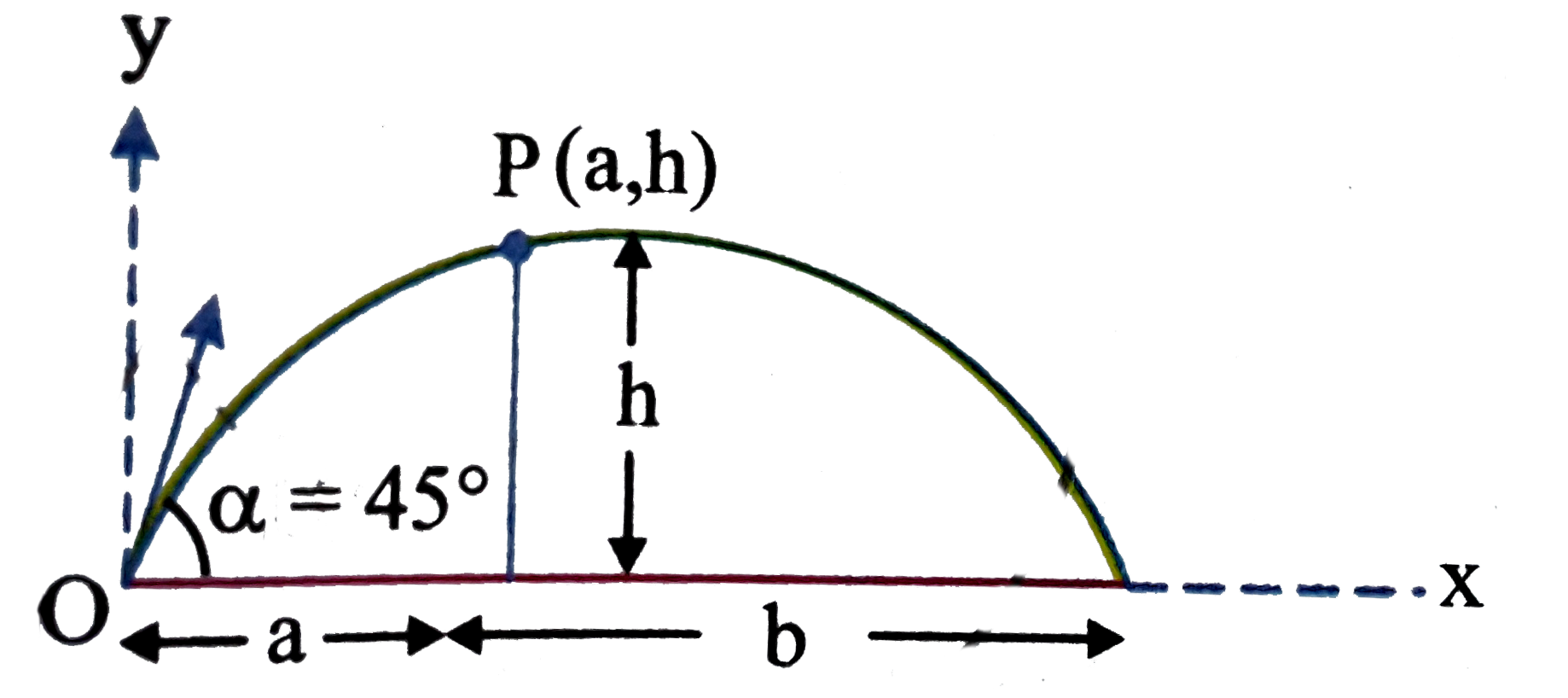
From a point on the ground at a distance $a$ from the foot of a pole, a ball is thrown at an angle of $45^{\circ}$ , which just touches the top of the pole and strikes the ground at a distance of $b$ , on the outer side of it. Find the height of the pole.

$\frac{a b}{a - b}$

$\frac{a b}{a + b}$

$\frac{2 a b}{a + b}$

$\frac{a b}{a + 2 b}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

From a point on the ground at a distance of 2m from the fot of a verticle wal, a ball is thrown at an angle of $45^{\circ}$ which just clears the top of the wall and then strikes the ground at distance of 4m from the foot of the wall on the other side. The height of the wall is
A3m
B $2 / 3 m$
C $3 / 4 m$
D $4 / 3 m$
A body is projected at an angle of $45^{\circ}$ with horizontal from a point on ground at distance $6 m$ from the foot of a vertical pole. It just crosses the top of the pole and falls on ground on the other side at a distance of $3 m$ from the foot of the pole. The height of the pole is:
A $1 m$
B $2 m$
C $3 m$
D $4 m$
A ball projected from ground at an angle of $45^{\circ}$ just clears a wall infront. If point of projection is $4 m$ from the foot of wall and ball strikes the ground at a distance of $6 m$ on the other side of the wall, the height of the wall is
A $4.4 m$
B $2.4 m$
C $3.6 m$
D $1.6 m$