A fixed morter fires a bomb at an angle of 53∘ above the horizontal with a muzzle velocity of 80ms−1. A tank is advancing directly towards the mortar on level ground at a constant speed of 5m/s. The initial separation (at the instant mortar is fired) between the mortar and tank, so that the tank would be hit is [Takeg=10ms−2]
662.4m
526.3m
486.6m
678.4m
The correct Answer is:D
d=R+x
R=614.4
T=12.8sec
AB=(5)12.8sec=64m
d=614.4+64
=678.4m
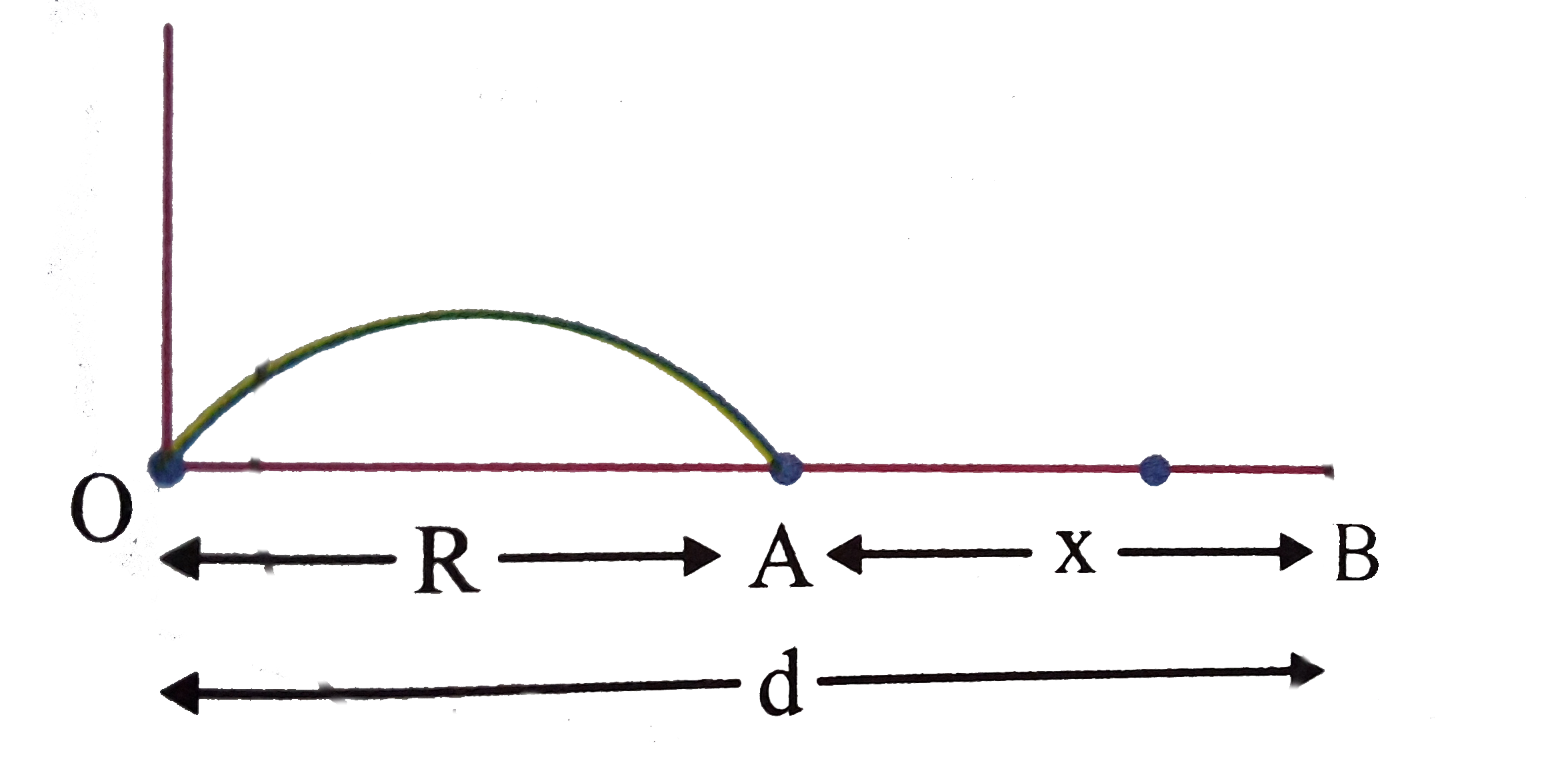
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Multi answer
18 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Passage
15 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. PASSAGE
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
Similar Questions
A 24−kg projectile is fired at an angle of 53∘ above the horizontal with an initial speed of 50m/s. At the highest point in its trajectory, the projectile explodes into two fragments of equal mass, the first of which falls vertically with zero initial speed.
(a) How far from the point of firing does the second fragment strike the ground? (Assume the ground is level.)
(b) How much energy was released during the explosion?
View SolutionA bullet fired from a gun with a velocity of 140ms−1 strikes the ground at the same level as the gun at a distance of 1 km. Find the angle of inclination with the horizontal at which the bullet is fixed. Take g=9.8ms−2.
View Solution
Knowledge Check
A projectile is thrown with a velocity of 10ms−1 at an angle of 60∘ with horizontal. The interval between the moments when speed is √5gm/s is (Take, g=10ms−2)
A1sB3sC2sD4sAn object is thrown towards the tower which is at a horizontal distance of 50 m with an initial velocity of 10ms−1 and making an angle 30∘ with the horizontal. The object hits the tower at certain height. The height from the bottom of the tower, where the object hits the tower is (Take, g=10ms−2)
A50√3[1−10√3]mB503[1−10√3]mC100√3[1−10√3]mD1003[1−10√3]mConsider a shell that has a muzzle velocity of 45ms−1 fired from the tail gun of an airplane moving horizontally with a velocity of 215ms−1 . The tail gun can be directed at any angle with the vertical in the plane of motion of the airplane. The shell is fired when the plane is above point A on ground, and the plane is above point B on ground when the shell hits the ground. (Assume for simplicity that the Earth is flat)
AShell may hit the ground at point A.BShell may hit the ground at point B.CShell may hit a point on earth which is behind point A.DShell may hit a point on earth which is behind point B.
A golfer standing on level ground hits a ball with a velocity of u=50ms−1 at an angle θ above the horizontal.If tanθ=512 then the time for which the ball is at least 15m above the ground will be take g=10ms−2
View SolutionWhat are the angles of projection of a projectile projected with velocity 30ms−1, so that the horizontal range is 45 m ? Take g=10ms−2.
View SolutionA lift, initially at rest on the ground, starts ascending with constant acceleration 8m/s2 After 0.5 seconds, a bolt falls off the floor of the lift. The velocity of the lift at the instant the bolt hits the ground is m/s .[Take g=10m/s2]
View SolutionThe water level on a tank is 5m high. There is a hole of 1cm2 cross-section at the bottom of the tank. Find the initial rate with which water will leak through the hole. (g=10ms−2)
View SolutionA projectile thrown with an initial velocity of 10ms−1 at an angle with the horizontal, has a range of 5 m. Taking g=10 ms−2 and neglecting air resistance, what will be the estimated value of α ?
View Solution
