Motion of a particle is governed by following relations y=xα,Vx=b−ct.(a,b,care+veconst)
The displacement (S) verson from (t) graph os
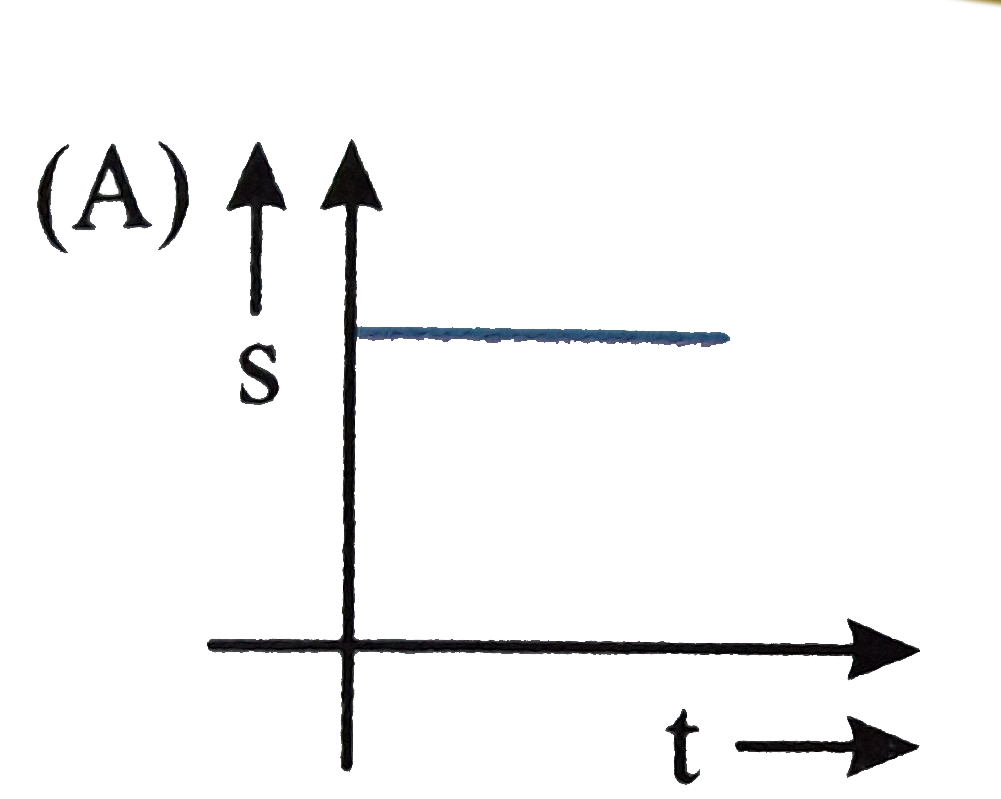
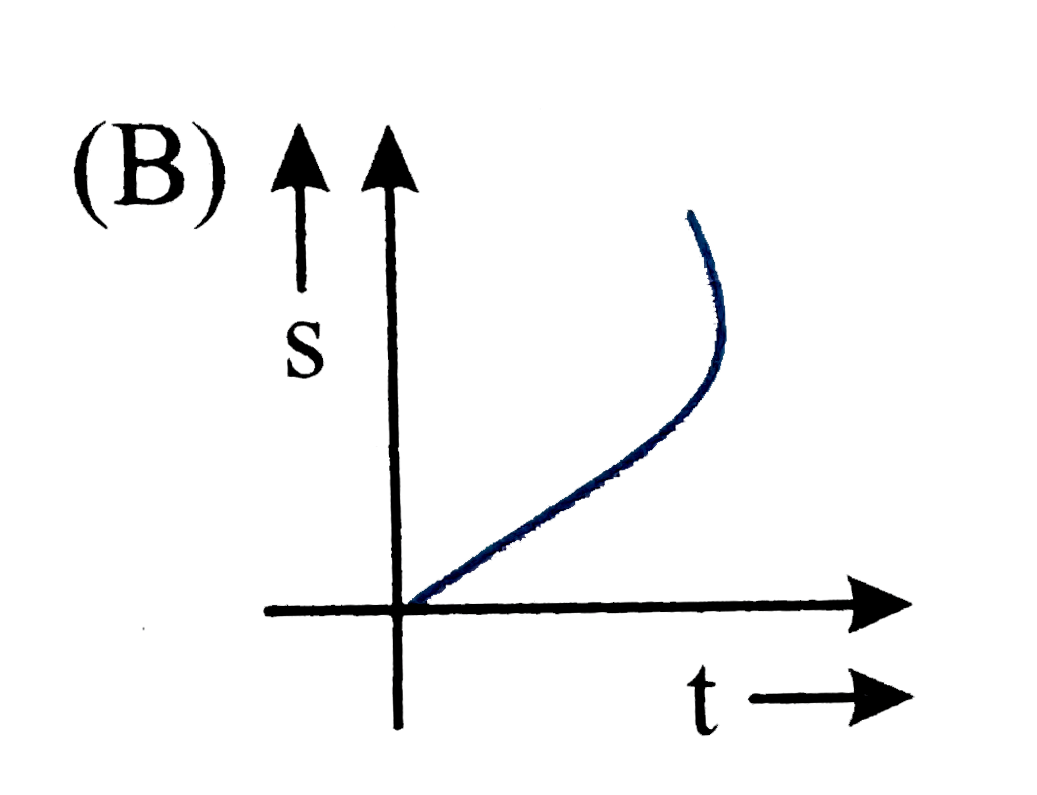
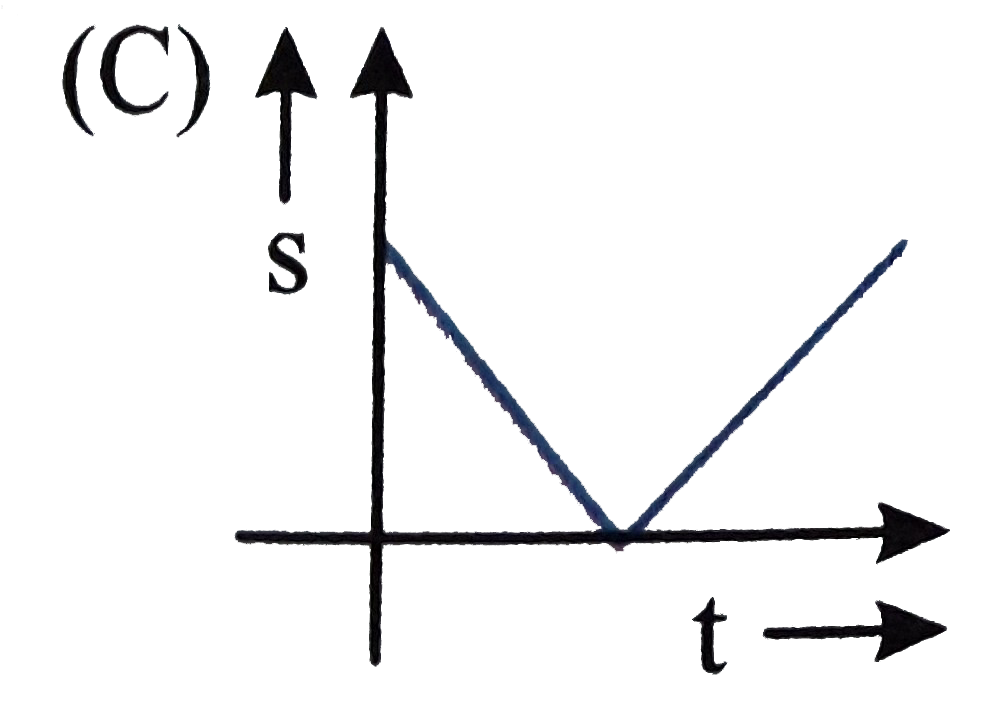
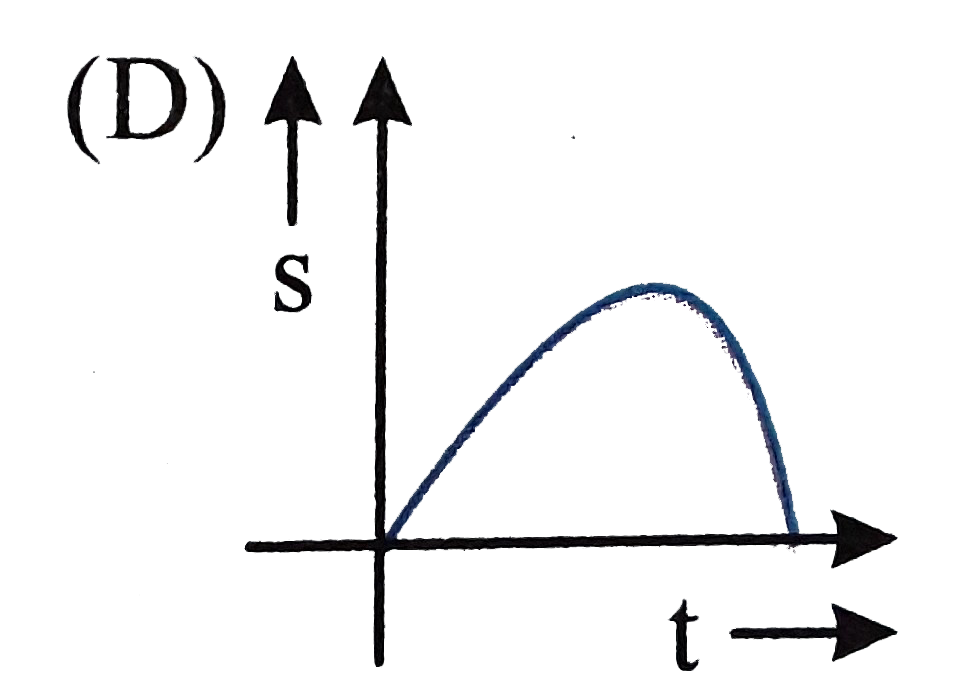
The correct Answer is:D
y=xα,Vx=b−ct,y=xα.⇒x=bt−12ct2
s=√x2+y2=√x2+x2α2,x√a+aa2
S=√1+1a2(bt−12ct2)
=kbt−kc2.t2(k=√1+1α2)
Parabolic curve
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Multi answer
18 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Passage
15 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. PASSAGE
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
Similar Questions
The positive of a particle at time t is given by the relation x(t)=(v0α)(1−c−αt), where v0 is a constant and α>0
The dimensions of v0 and α are respectively
View SolutionThe motion of a particle is given by a straight line in the graph given above drawn with displacement (x) and time (t). Which one among the following statements is correct ?
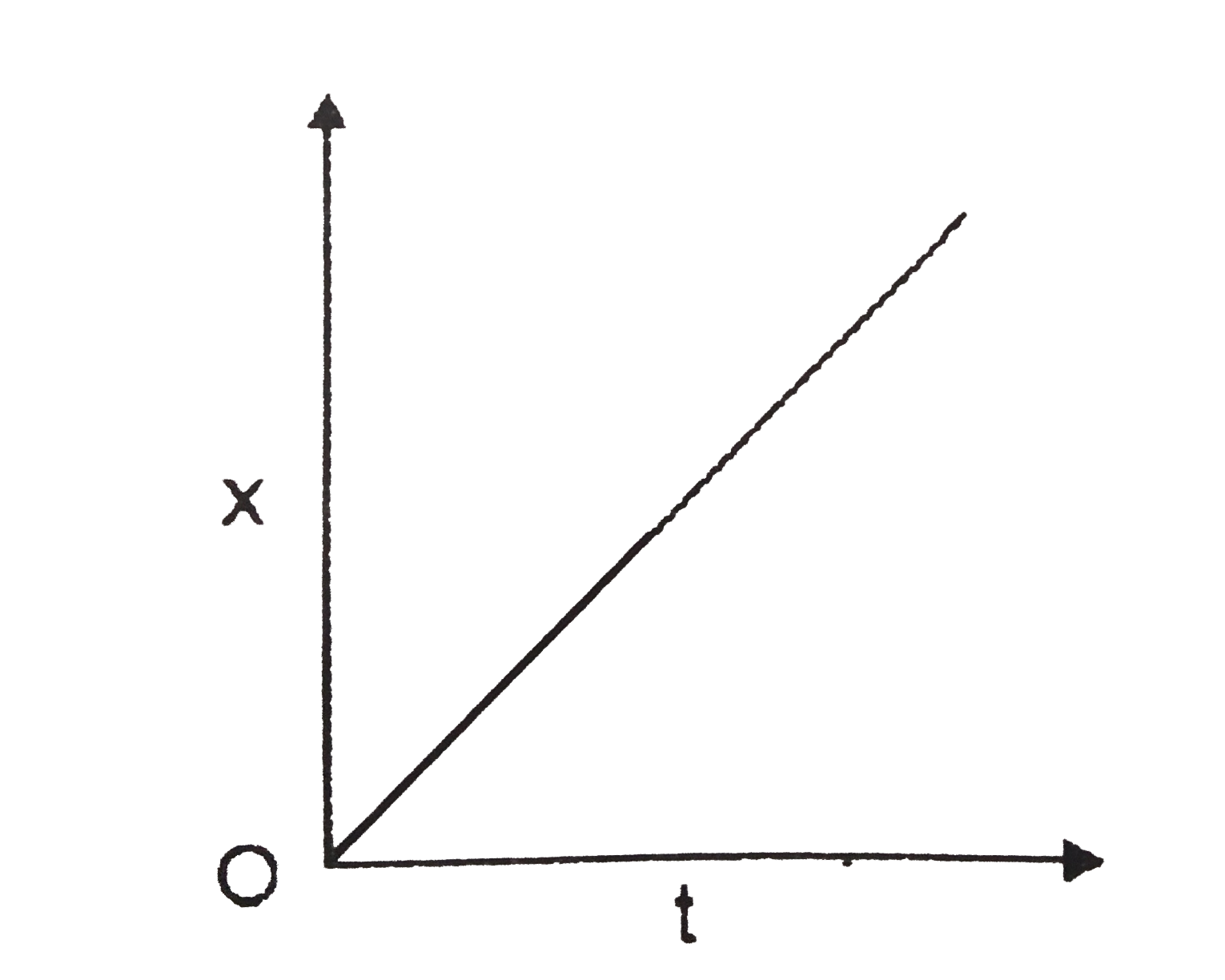
View Solution
Knowledge Check
The motion of a particle is given by x=Asinωt+Bosωt. The motion of the particle is
Anot simple harmonicBsimple harmonic with amplitude A+BCsimple harmonic with amplitude (A+B2)Dsimple harmonic with amplitude √A2+B2The position of a particle at time t is given by the relation x(t)=(v0α)(1−c−at), where v0 is a constant and α>0. Find the dimensions of v0andα.
A[L−1T−1],[T−2]B[L2T−1],[T−1]C[LT−1],[T−1]D[LT−2],[T1]A particle is moving in x−y plane with y=x2 and Vx=4−2t. The displacement versus time graph of the particle would be
A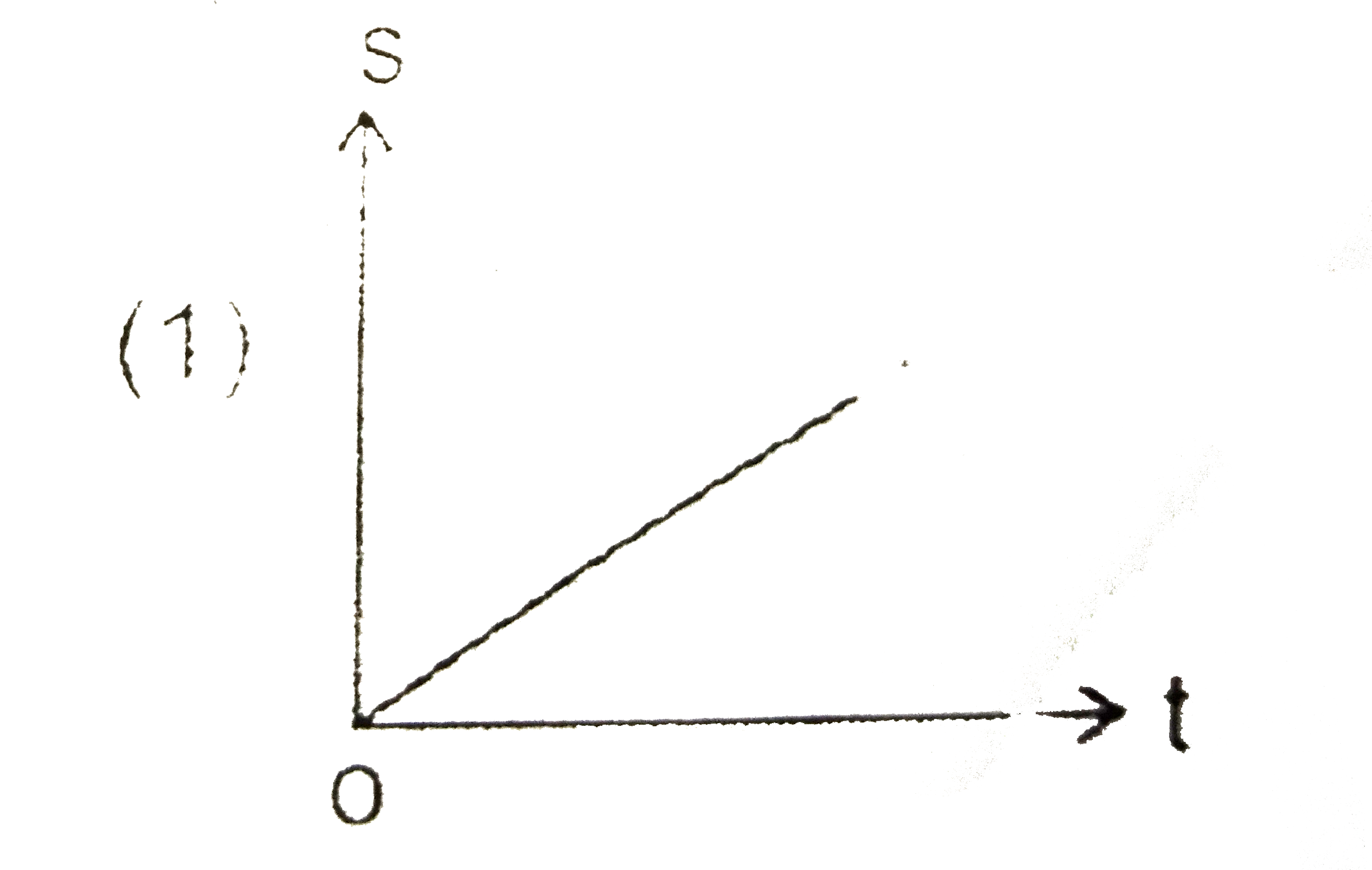 B
B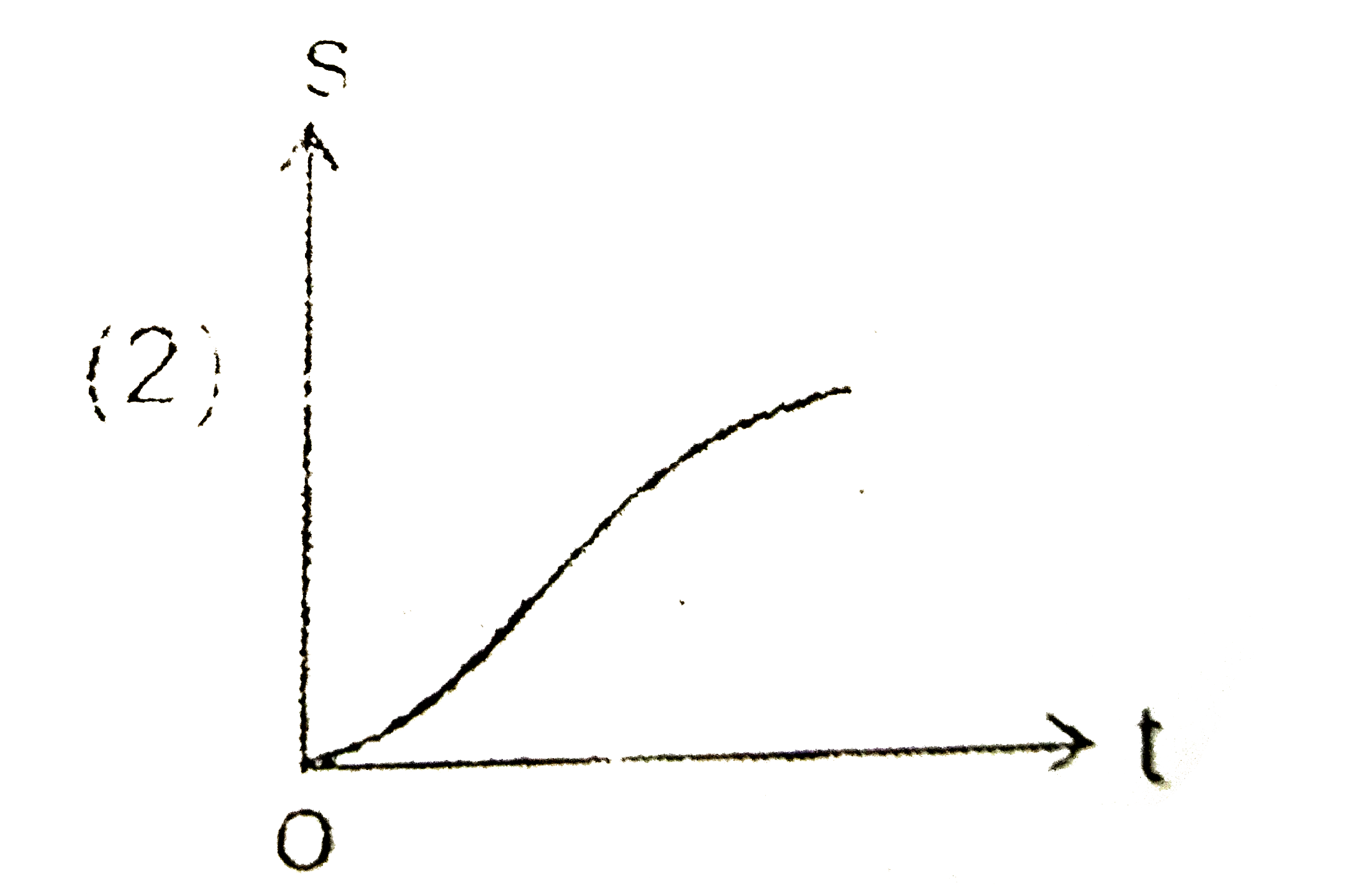 C
C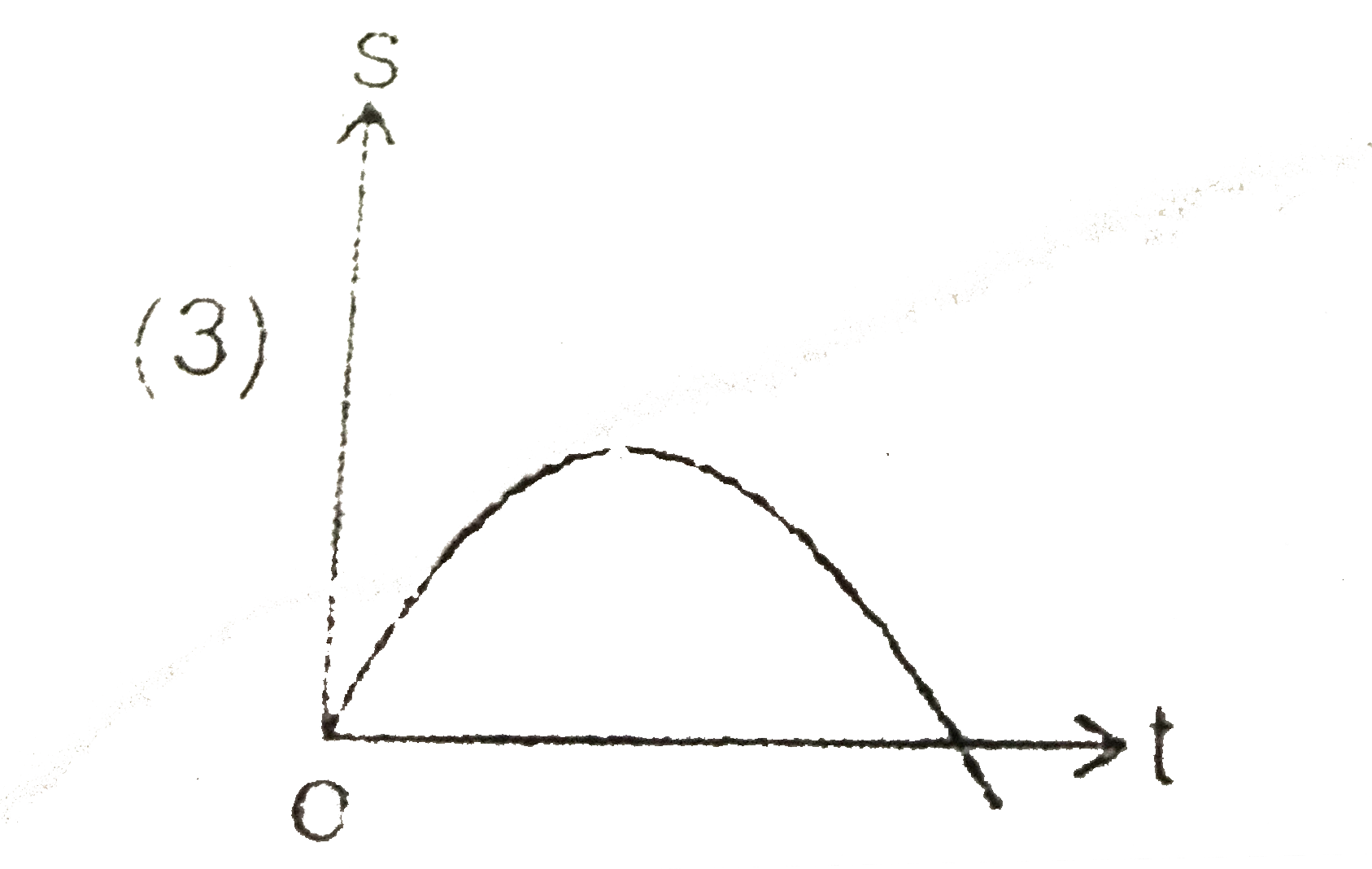 D
D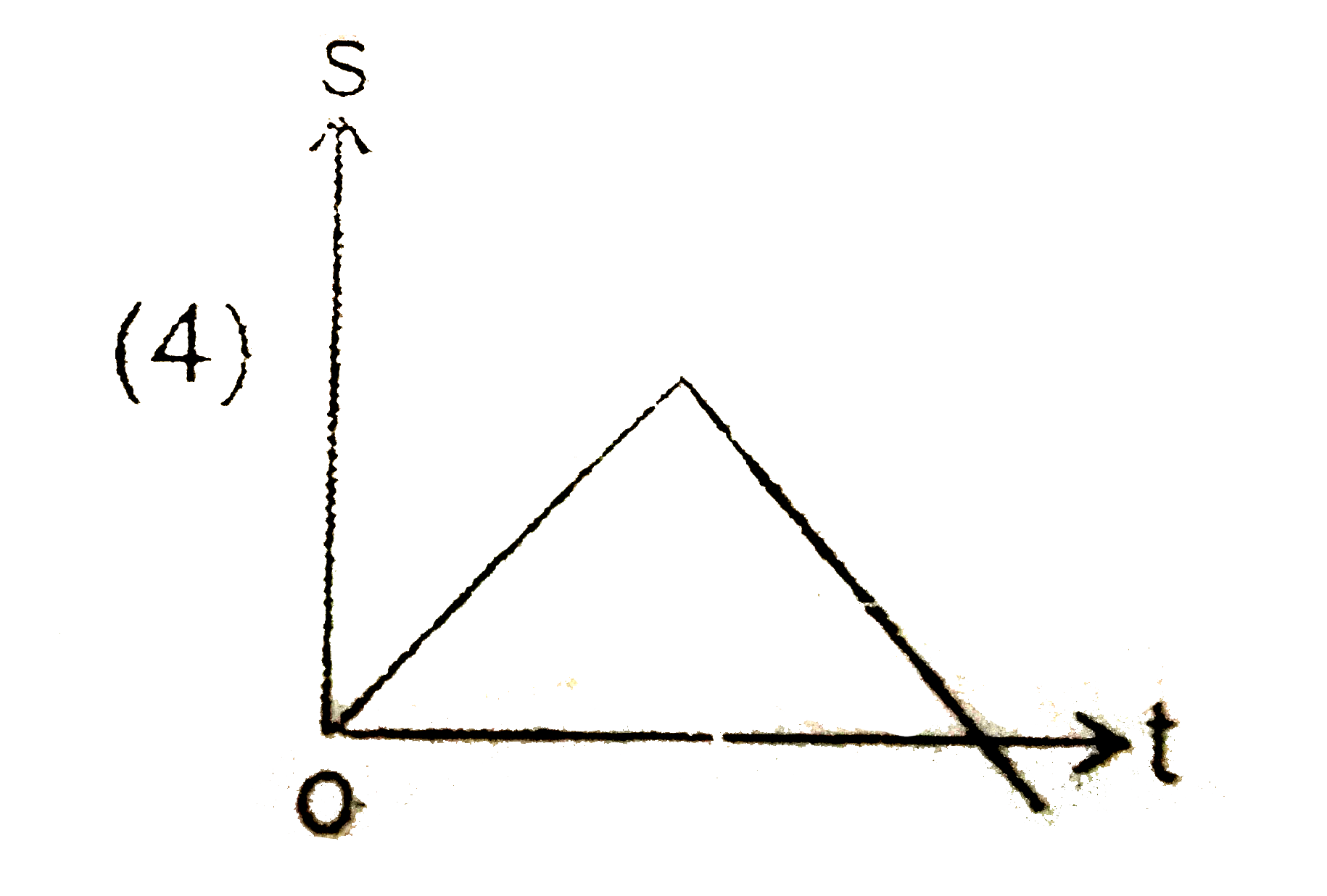
The position of a particle at time t is given by the relation x(t)=(v0α)(1−e−αt) where v0 is a constant and α>0. Find the dimensions of v0 and α
View Solutions-t graph of a particle in motion is shown in Fig. Calculate
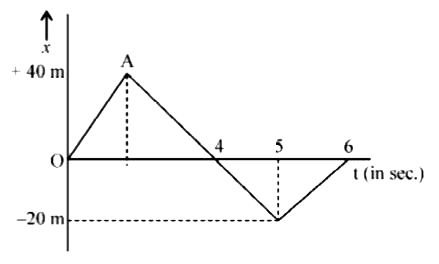
Displacement
View SolutionThe motion of a particle is given by x=Asinωt+Bcosωt. The motion of the particle is
View SolutionThe position-time relation of a particle moving along the x-axis is given by
x=a−bt+ct2
where a, b and c are positive numbers. The velocity-time graph of the particle is
View SolutionThe displacement of a particle is represented by the equation y=3cos(π4−2ωt).
The motion of the particle is
View Solution
