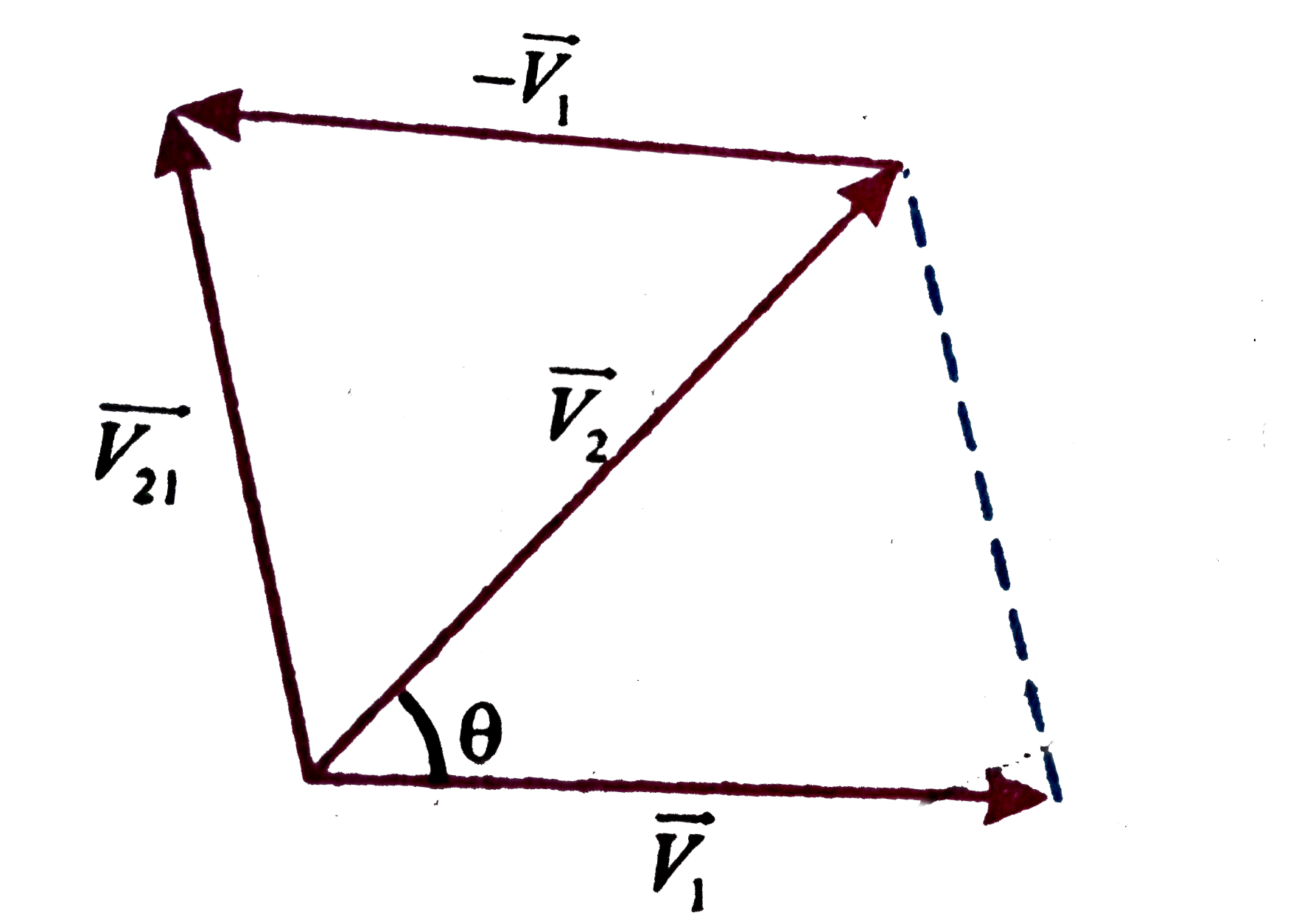
Consider a collection of a large number of particles each with speed in a plane.The direction of velocity is randomly distributed in the collection.The magnitude of the average relative velocity of a particle with velocities of all other particles is
none of these
The correct Answer is:A
Let and are the velocity of any two particles and is the angle between them.As each particles has same speed, so
The relative velocity of particle w.r.t is given by
As the velocities of the particles are randomly distributed, so varies from to .The magnitude of average velocity when averaged over all such pairs, Thus
.
Topper's Solved these Questions
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level -V Multi answer
Explore 18 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level -V Passage
Explore 15 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:NCERT BASED QUES. PASSAGE
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
Similar Questions
Consider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
View SolutionHow does particle velocity differ from wave velocity?
View Solution
Knowledge Check
A large number of particles are moving each with speed v having directions of motion randomly distributed. What is the average relative velocity between any two particles averaged over all the pairs?
AvB(π/4)vC(4/π)vDZeroAverage velocity of the particle for the motion
A3.3 m/sB6.7 m/sC2.7 m/sD7.6 m/sIn the pervious question ,what is the average velocity of the particle?
A1ms−1B0.5ms−1C3ms−1DNone of these
A particle is doing uniform circular motion as shown. Magnitude of average velocity of the particle between points A and C will be
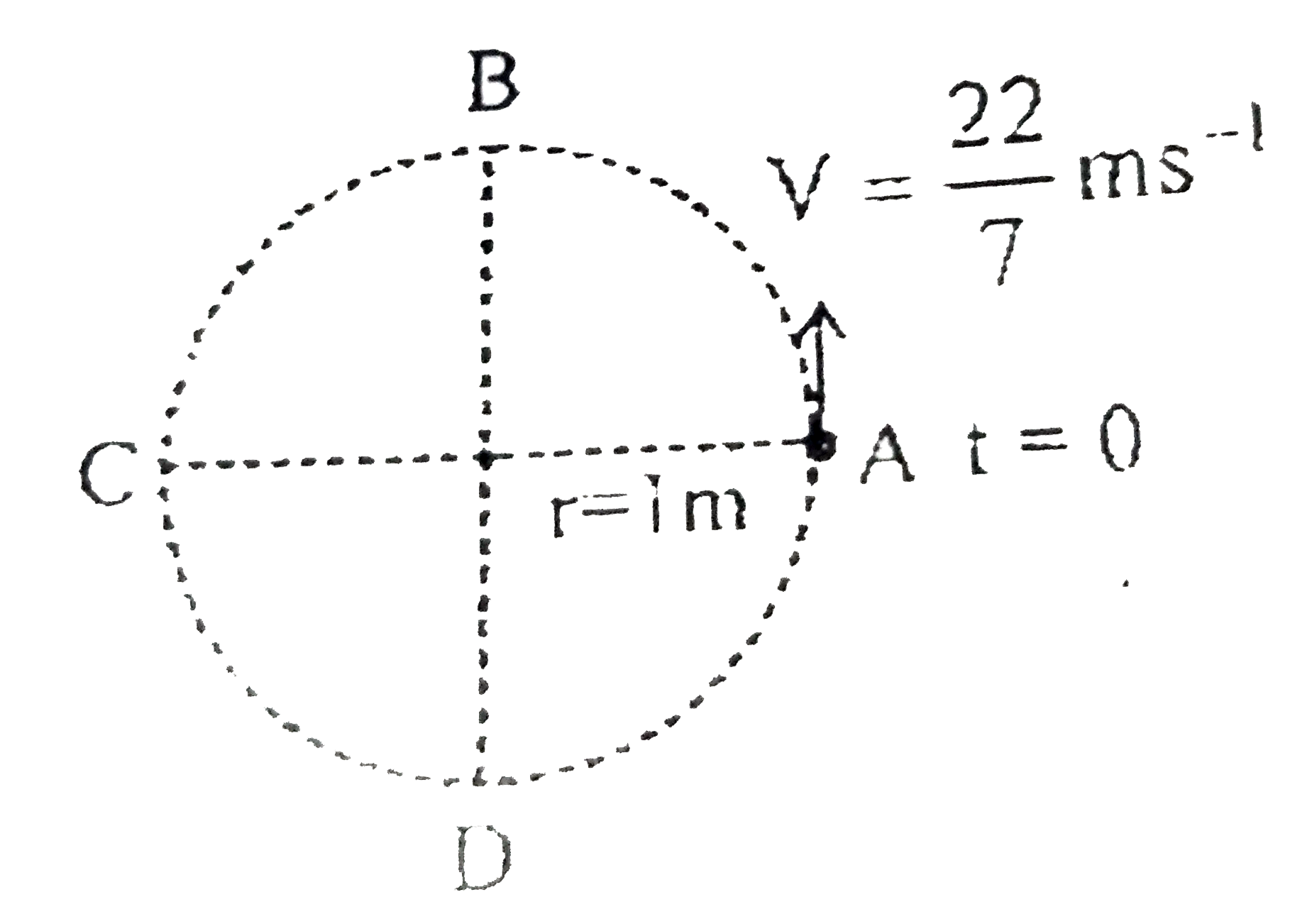
View SolutionIn Q.36, average velocity during the motion of the particle is.
View SolutionThe magnitude of average velocity is equal to the average speed when a particle moves:-
View SolutionA particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
View SolutionIn the previous question, the magnitude of velocity of particle at the mentioned instant is
View Solution

