A particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
2v
v(vπ)
v2
v2π
The correct Answer is:B
To find the magnitude of the average velocity of a particle moving with constant speed v in a circle after half a rotation, we can follow these steps:
1. Understand the Motion:
The particle moves in a circular path. Let's denote the center of the circle as point O and the starting point as point A. After half a rotation, the particle will reach point B, which is directly opposite point A on the circle.
2. Determine the Displacement:
The displacement is the straight-line distance between the starting point A and the endpoint B. Since points A and B are diametrically opposite in the circle, the displacement can be calculated as the diameter of the circle.
Displacement=AB=2r
where r is the radius of the circle.
3. Calculate the Time Taken:
To find the average velocity, we need to determine the time taken to move from A to B. The distance traveled in half a rotation is half the circumference of the circle.
Distance traveled=12×2πr=πr
The time taken to travel this distance at speed v is:
Time=DistanceSpeed=πrv
4. Calculate the Average Velocity:
The average velocity is defined as the total displacement divided by the total time taken.
Average Velocity=DisplacementTime=2rπrv=2r⋅vπr=2vπ
5. Final Result:
Therefore, the magnitude of the average velocity after half a rotation is:
Average Velocity=2vπ
The particle moves in a circular path. Let's denote the center of the circle as point O and the starting point as point A. After half a rotation, the particle will reach point B, which is directly opposite point A on the circle.
The displacement is the straight-line distance between the starting point A and the endpoint B. Since points A and B are diametrically opposite in the circle, the displacement can be calculated as the diameter of the circle.
Displacement=AB=2r
where r is the radius of the circle.
To find the average velocity, we need to determine the time taken to move from A to B. The distance traveled in half a rotation is half the circumference of the circle.
Distance traveled=12×2πr=πr
The time taken to travel this distance at speed v is:
Time=DistanceSpeed=πrv
The average velocity is defined as the total displacement divided by the total time taken.
Average Velocity=DisplacementTime=2rπrv=2r⋅vπr=2vπ
Therefore, the magnitude of the average velocity after half a rotation is:
Average Velocity=2vπ
Topper's Solved these Questions
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE WORKOUT (CATEGORY 2: SINGLE OPTION CORRECT TYPE (2 MARKS))
15 Videos
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE WORKOUT (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
10 Videos
- KINETIC THEORY OF GASES BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)
7 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - MTG-WBJEECHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - WB JEE Previous Years Questions
22 Videos
Similar Questions
A particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View SolutionA particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
View Solution
Knowledge Check
A particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is
 Av√a2+b2BvbCvb(a2+b2)Dva
Av√a2+b2BvbCvb(a2+b2)DvaA particle is moving in a circle with a constant speed. Its moving is
APeriodicBOscillatoryCSimple harmonicDboth 'a' and 'b'A particle is moving with a constant speed in a circular orbit. Find the change in its velocity when it completes half the revolution.
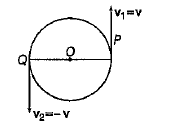 A2vB4vC3vDv
A2vB4vC3vDv
A particle of mass m moves with constant speed v on a circular path of radius r. Find magnitude of average force on it in half revolution.
View SolutionA particle is moving along a circular path with a constant speed 10ms−1.What is the magnitude of the change in velocity of the particle ,when it moves through an angle of 60∘ around the center of the circle ?
View SolutionAre the magnitudes of average velocity and average speed equal?
View SolutionA particle is moving on a circular path with constant speed v. The magnitude of the change in its velocity after it has described an angle of 90∘ is :
View SolutionA particle moves with a speed v in a circle of radius R.The x-component of the average velocity of the particle in a half- revolution, as shown in figure−3.76,is:
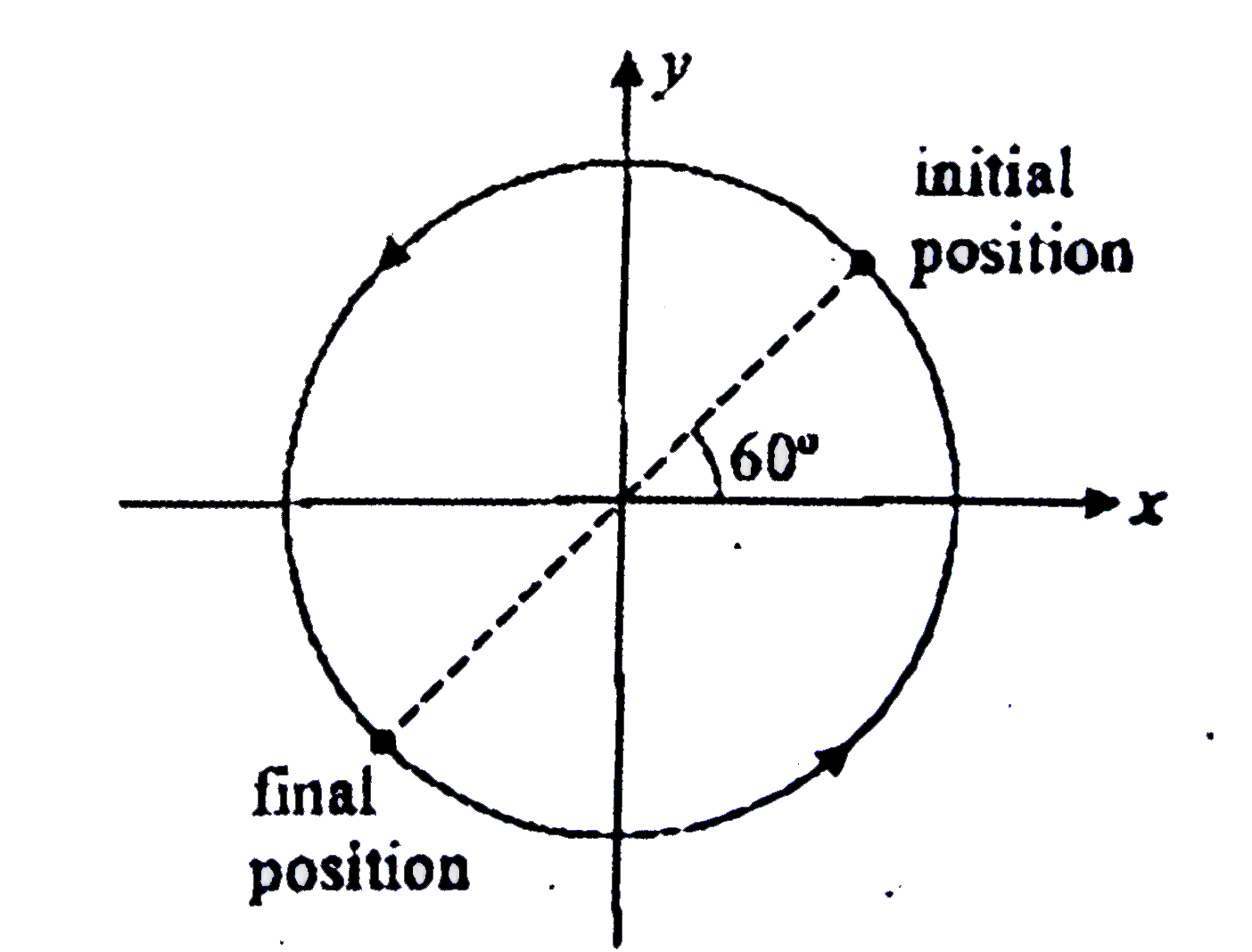
View Solution
