In the previous question, let the ring have non-uniformly distributed charge, and let it be spinning about its axis. Let F be the net force on the ring and τ be the torque on the ring due to the straight conductor
F≠0,τ≠0
F=0,τ≠0
F≠0,τ=0
F=0,τ=0
The correct Answer is:D
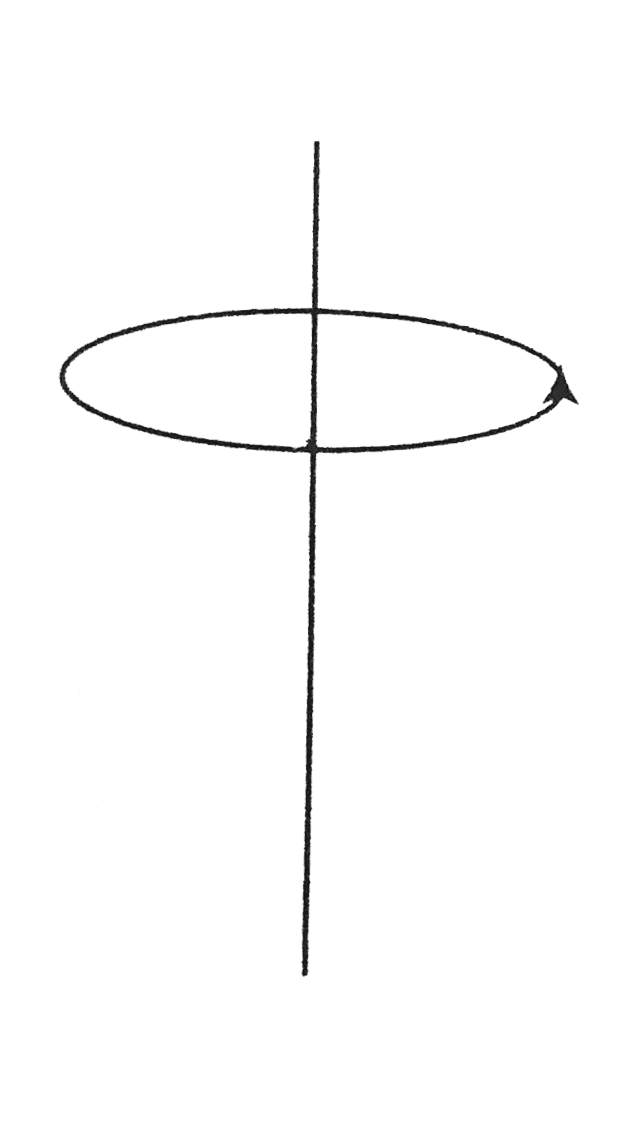
Let charge on ring is q,I=qT=q2π/ω=qω2π
Due to long wire, magnetic field will be uniform.
force on ring =0
The directed of magnetic moment and magnetic field will be θ=0∘ or 180∘
τ=0
Topper's Solved these Questions
Similar Questions
Electric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b. perpendicular to the plane of the ring.
View Solution
Knowledge Check
A non conducting rod AB of length √3R, uniformly distributed charge of linear charge density λ and a non-conducting ring of uniformly distributed charge Q, are placed as shown in the figure. Point A is the centre of ring and line AB is the axis of the ring, perpendicular to plane of ring. The electrostatic interaction energy between ring and rod is
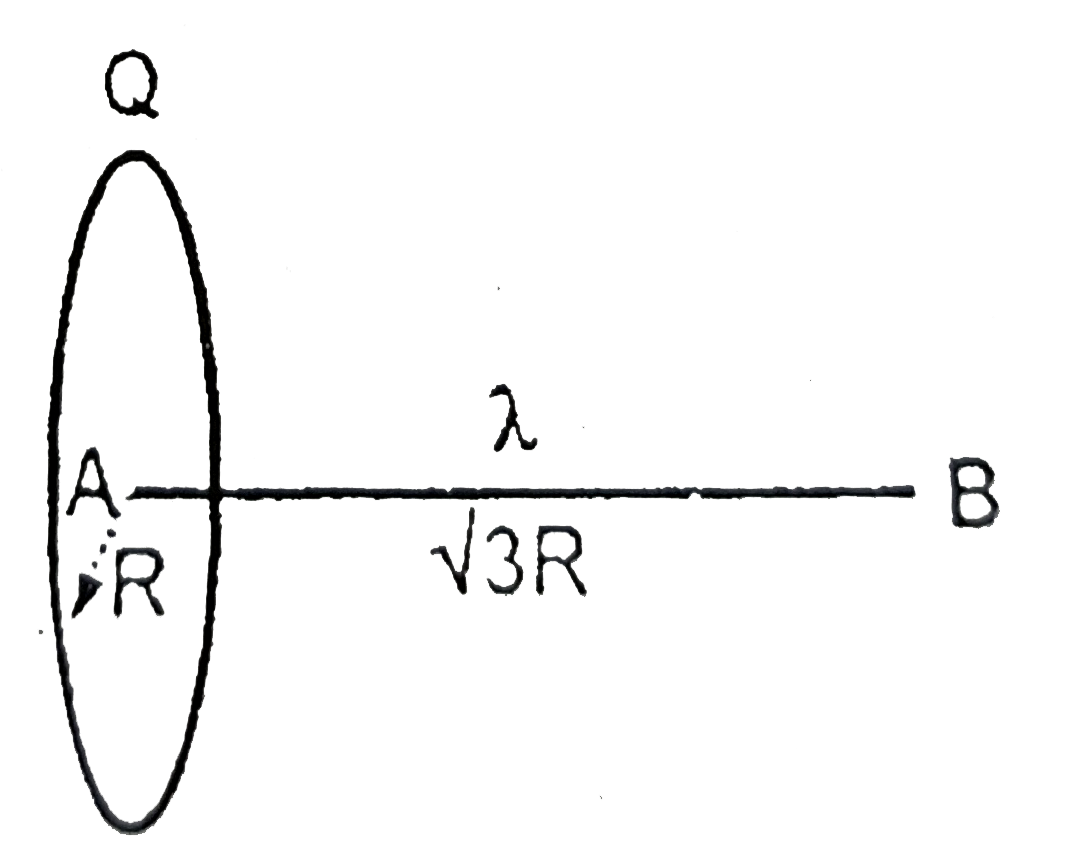 AQλ4πε0ln(2+√3)BQλ2πε0ln(2+√3)CQλ4πε0ln(2−√3)DQλ2πε0ln(2−√3)
AQλ4πε0ln(2+√3)BQλ2πε0ln(2+√3)CQλ4πε0ln(2−√3)DQλ2πε0ln(2−√3)A charge of 5 nC is uniformly distributed on a ring of radius 4 cm. Find the potential at the axis at a distance of 3 cm from the center.
A0.09VB600 VC900 VD300 VA closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
Let ring in the above question is having a radius R and a charge Q is uniformly distributed over it. Ring is rotated with a constant angular velocity (ω) as mentioned above.
Torque acting on the ring due to magnetic force isAQR2ωB2BQR2ωB2ωCωR2B2πDNone of the above
Calculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of readius R.
View SolutionMass is non - uniformly distributed on the circumference of a ring of radius a and centre at origin . Let b be the distance of centre of mass of the ring from origin. Then ,
View SolutionA charge q is uniformly distributed over the surface of a ring-shaped conductor of radius a. Find the field intensity on the axis of the conductor at a distance x from the plane of the conductor.
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA non conduction ring of raducs R Has uniformly distributed positive charge Q.A small part of the ring of length d, is removed (d lt lt R) . The electric field at the centre of the ring now be .
View Solution

