Two insulated rings, one of a slighlty smaller diameter than the other are suspended along their common diameter as shown. Initially the planes of the rings are mutually perpendicular. When a steady current is set up each of them
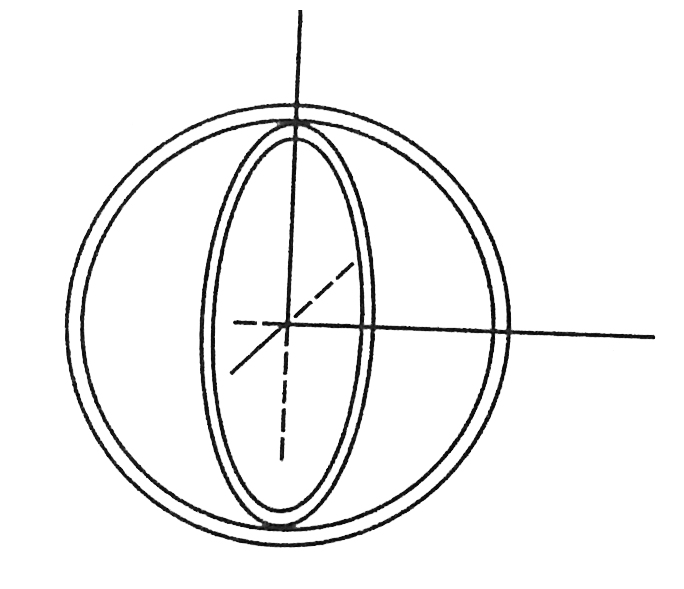
The two rings rotate into a common plane
The inner rings oscillates about its initial position
The inner ring stays stationary while the outer one moves into the plane of the inner ring
The outer ring stays stationary while the inner one moves into the plane of the outer ring
The correct Answer is:A
The torque will be exerted on rings.
Topper's Solved these Questions
Similar Questions
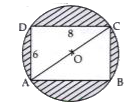
Two coins of diameter 2 cm and 4 cm respectively are kept one over the other as shown in the figure the area of the shaded ring shaped region is ___ square cm.
View SolutionAt the centre of a fixed large circular coil of radius R a much smaller circular coil of radius r is placed .The two coils are concentric and are in the same plane .The larger coil carries a current I The smaller coil is set to rotate with a constant angular velocity ω about an axis along their common diameter .Calculate the emf induced in the smaller coil after a time t of its start of ratation
View Solution
Knowledge Check
There are two concentric circular loops. One loop of radius r is made up of only one turn. The other loop has a radius 2r and has two turns of wire. They are arranged such that they have a common centre and their planes are perpendicular to each other. When the same current i is passed through both the coils, the magnetic field at the common centre is
Aμ0i2rBμ0irCμ0i2r√2DzeroThe moment of intertia of a disc about an axis passing through its centre and normal to its plane is I. The disc is now folded along a diameter such that the two halves are mutually perpendicular. Its moment of inertia about this diameter will now be
AIBI√2CI2DI4The radius of a circular ring of wire is R and it carries a current of I ampere. At its centre a smaller ring of radius r with current i and N turns is placed. Assuming that the planes of two rings are perpendicular to each other and the magnetic induction produced at the centre of bigger ring is constant, then the torque acting on smaller ring will be -
ANiπr2×{μ0I2R}BzeroCNir2×{μ0I2R}DNir2{I22R}
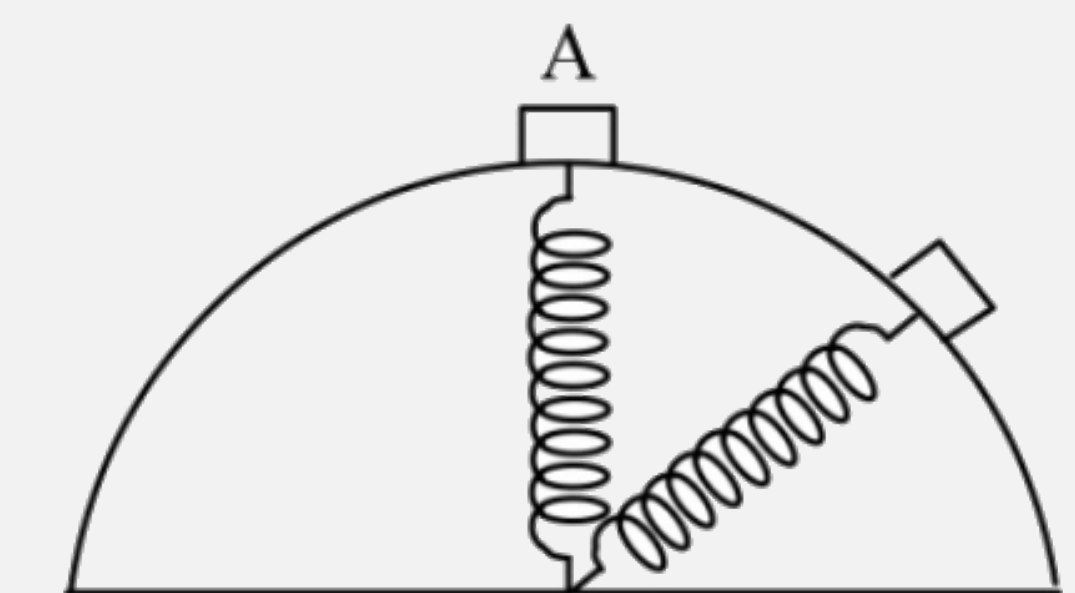
A bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
View SolutionA circular coil of Radius R is folded across its diameter such that the planes of two half rings are perpendicular to each other as shown in the figure. If the current through the coil is calculate the magnetic dipole moment of the configuration so formed.
View SolutionTwo circular rings each of mass M and radius R are attached to each other at their rims and their planes perpendicular to each other as shown in figure. The moment of inertia of the system about a diameter of one of the rings and passing through the point of contanct is

View SolutionIn a ring ABCD of radius r, the lower half ABC has mass m and the upper half ADC has mass 2m. In both parts, the masses are distributed evenly. The ring is initially at rest on a horizontal surface, as shown. O is the centre of the ring.

The ring is now folded along the diameter AC, such that the plane of the section ABC is normal to the plane of the section ADC. (The angle BOD =90∘). It is then placed on a thin, fixed horizontal wire, ie.e, the diameter AC lies along the wire. The angle made by DO with the vertical will now be
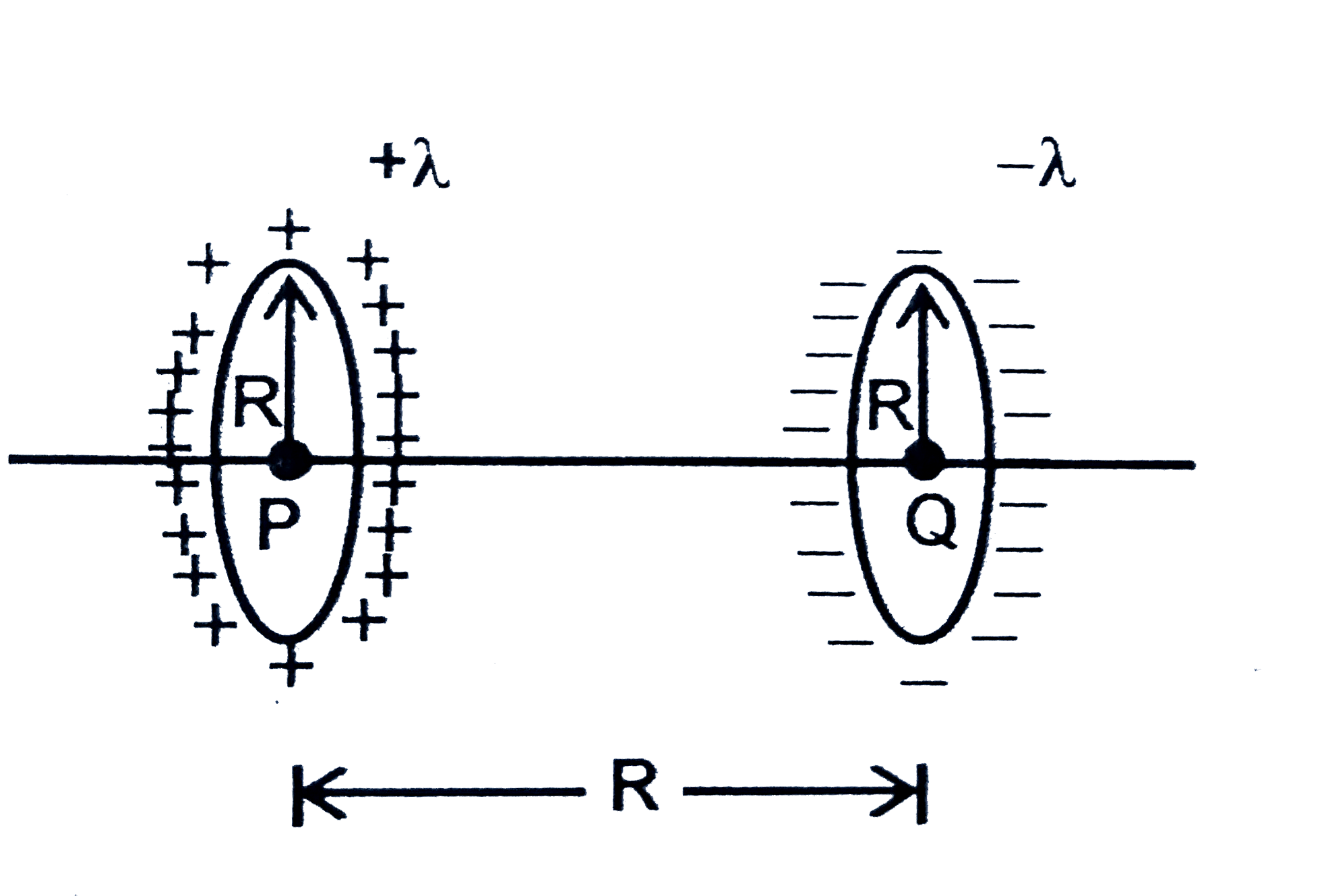
View SolutionTwo fixed insulating rings A and B carry ahanges with uniform linear aharge density +λ and −λ, respectively, as shown in the adjacent figure. The planes of the rings are parallel to each other and their axes are coinciding. A particle of change "q" and mass "m" is released with zero velocity from centre P of the positively charged ring. The kinetic energy of the particle when it reaches centre Q of the negatively charge ring will be
View Solution

