Find the out the moment of inertia of a ring having uniform mass distribution of mass $M$ and radius $R$ about an axis which is tangent ot the ring and $a$ in the plane of the ring $b$ . perpendicular to the plane of the ring.

Video Solution

Text Solution

Verified by Experts

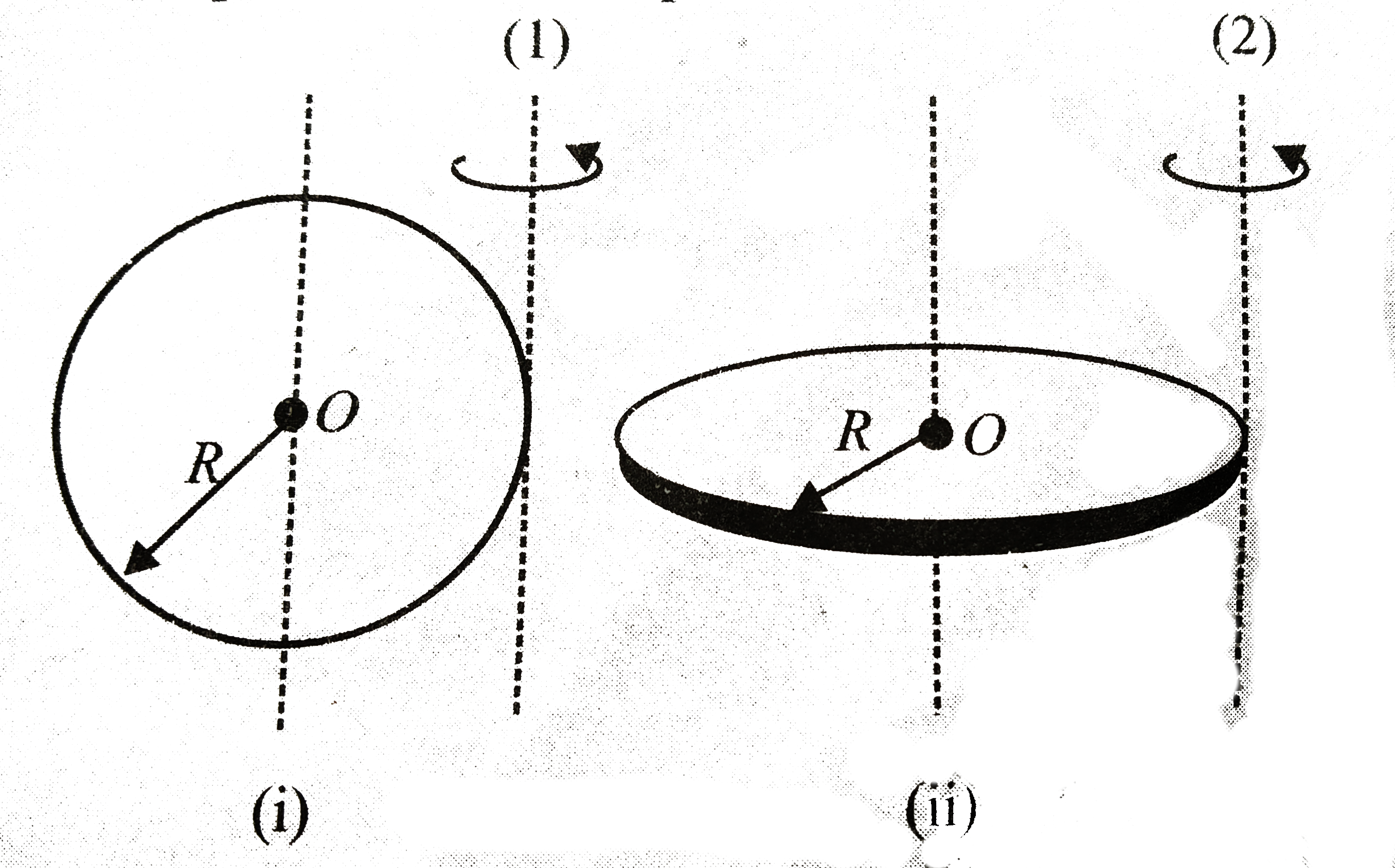
The moment of inertia of a ring about an axis passing through centre and perpendicular to plain of ring is $I_{x} = I_{y}$ and using perpendicular axis theorem.

$I_{z} = I_{x} + I_{y} \Rightarrow M R^{2} = 2 I_{x}$
$\Rightarrow I_{x} = \frac{M R^{2}}{2} = I_{0}$
For case a using parallel axis theorem
$I_{1} = I_{0} + \frac{M R^{2}}{2} + M R^{2} = \frac{3}{2} M R^{2}$
For case $b$ using parallel axis theorem,
$I_{2} = I_{z} + M R^{2} = M R^{2} + M R^{2} = 2 M R^{2}$

Updated on:21/07/2023

Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A $\frac{5}{2} M R^{2}$
B $\frac{3}{2} M R^{2}$
C $\frac{1}{2} M R^{2}$
D $M R^{2}$
Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A $M R^{2}$
B $\frac{1}{2} M R^{2}$
C $\frac{3}{2} M R^{2}$
D $\frac{7}{2} M R^{2}$
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A $1 / 2 M R^{2}$
B $M R^{2}$
C $1 / 4 M R^{2}$
D $3 / 4 M R^{2}$