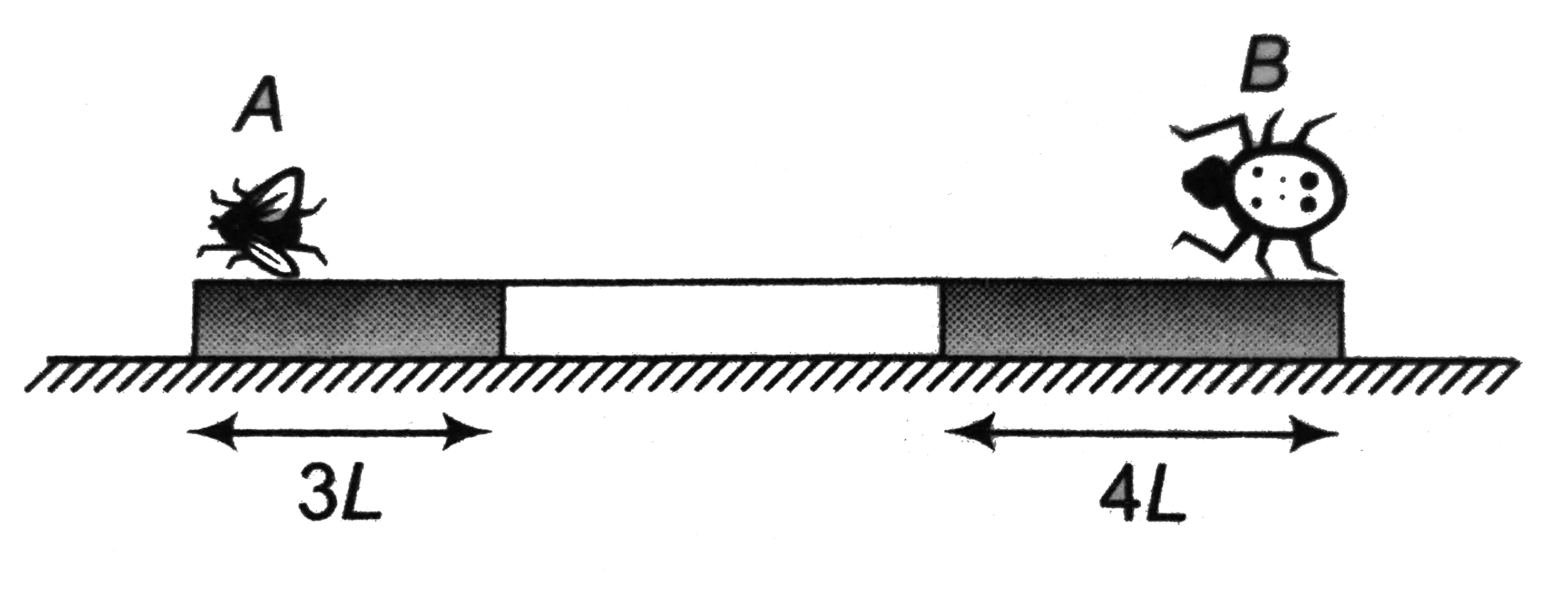
A uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v/2 relative to the rod towards the end A. The spider takes negligible time in eating the insect. Also, let v=L/T, where T is a constant having value 4sec.
The point P is at
the centre of the rod
the edge of the table supporting the end B
close to the edge of the table supporting the end A
none of the above
The correct Answer is:B
Displacement of moth =12L3×2=8L
∴ Point P is at the table supporting B.
Topper's Solved these Questions
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Subjective type Questions
Explore 9 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-I (H.W)
Explore 52 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Multiple Answer
Explore 11 Videos
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:LEVEL II(H.W)
Explore 51 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
Similar Questions
A uniform bar AB of length 6a has been placed on a horizontal smooth table of width 5 a as shown in the figure. Length 2a of the bar is overhanging. Mass of the bar is 4m. An insect of mass m is sitting at the end A of the bar. The insect walks along the length of the bar to reach its other end B.
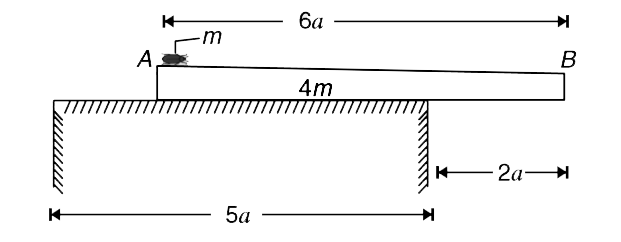
(a) Will the bar topple when the insect reaches end B of the bar ?
(b) After the insect reaches at B, another insect of mass M lands on the end A of the bar. Find the largest value of M which will not topple the bar.
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
By what distance the centre of mass of the rod shifts during this time?
View Solution
Knowledge Check
A uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v/2 relative to the rod towards the end A. The spider takes negligible time in eating the insect. Also, let v=L/T, where T is a constant having value 4sec.
The speed of the bar after the spider eats up the moth and moves towards A isAv/2BvCv/6D2vA uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v/2 relative to the rod towards the end A. The spider takes negligible time in eating the insect. Also, let v=L/T, where T is a constant having value 4sec.

Displacement of the rod by the time when the insects meet isAL/2BLC3L/4DzeroA uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
After starting from end B of the rod the spider reaches the end A at a timeA(a) 40sB(b) 30sC(c) 80sD(d) 10s
A uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA strip of wood mass M and length l is placed on a smooth horizontal surface. An insect of mass m starts from rest at one end of the strip and walks to the other end in time t, moving with a constant speed.
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision.
View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View Solution

