A small particle of mass m/10 is moving horizontally at a height of 3R/2 from ground with velocity 10m/s. A perfectly inelastic collision occurs at point P of surface. The mass m of sphere is R. (m=10Kg and R=0.1m) (Assume all surfaces to be smooth). Answer the following questions.

speed of particle just after collisons is approximately..........
5.0m/s
10m/s
15.0m/s
20.0m/s
The correct Answer is:A

Let v1 be the velocity of sphere after collision
Jcos30=10v1⇒J=20v1√3
J=m10(10cos30)−m10(v1cos30∘)
⇒ speed of the sphere v1=3043ms−1
speed of particle in tangential direction remains same
10sin30=5ms−1
speed of partile =√(5)2+[(3043)cos30]2
=5.26ms−1
Topper's Solved these Questions
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Subjective type Questions
Explore 9 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-I (H.W)
Explore 52 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Multiple Answer
Explore 11 Videos
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:LEVEL II(H.W)
Explore 51 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
Similar Questions
Two particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then

View SolutionA particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
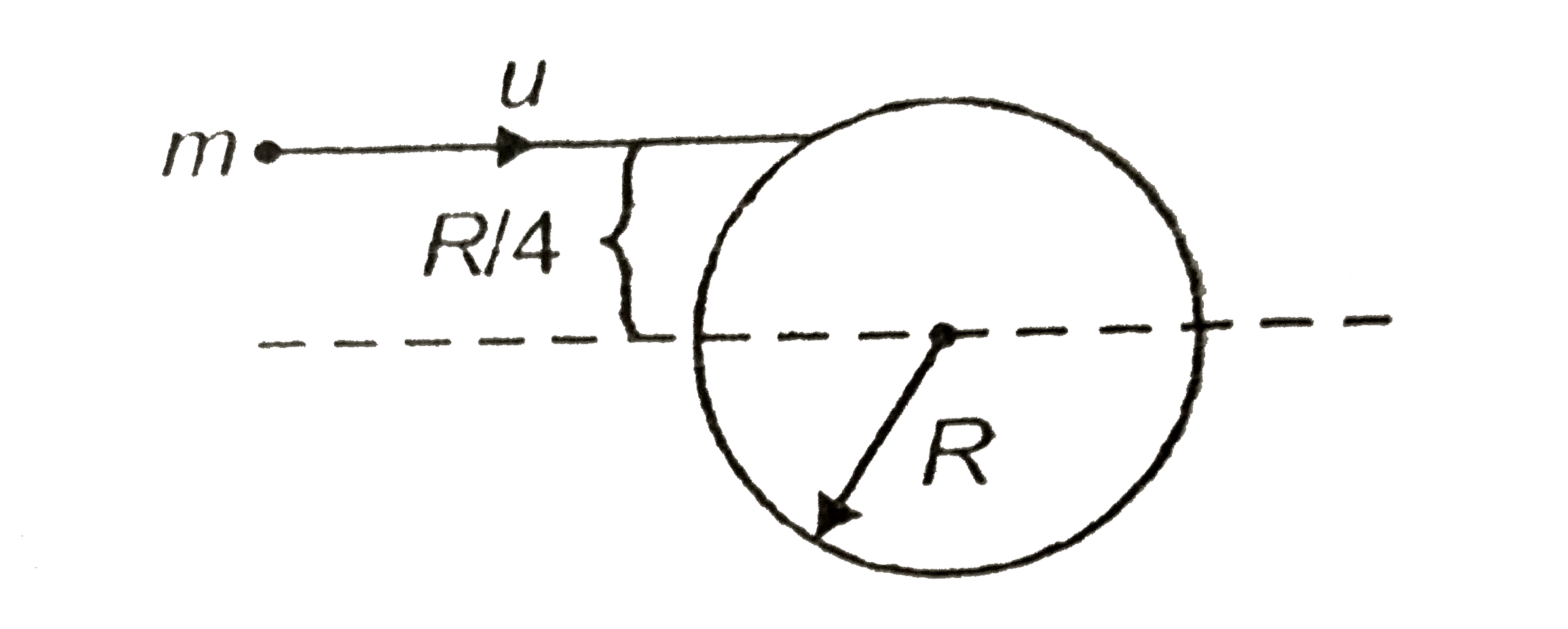
View Solution
Knowledge Check
A small particle of mass m/10 is moving horizontally at a height of 3R/2 from ground with velocity 10m/s. A perfectly inelastic collision occurs at point P of surface. The mass m of sphere is R. (m=10Kg and R=0.1m) (Assume all surfaces to be smooth). Answer the following questions.

Speed of shpere just after collision isA27/43m/sB3043m/sC3543m/sD4043m/sSphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.

At what height h above the floor, particle should hit the sphere so that it may start pure rolling after the collision.A5R7B3R5C3R7D7R5Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.

What will be the approximate velocity of combined system after the collision?AmuMBmu2MC2muMDzero
Two particles each of mass m moving with equal speed 2m/s along the indicated direction in the figure undergo a perfectly inelastic collision.Velocity of combined system after collision is ?
View SolutionA particle of mass m moving with horizontal speed 6m/s as shown in the figure. If m<<M then for one - dimensional elastic collision , the speed of lighter particle after collision will be

View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionSphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.
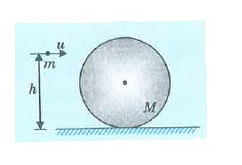
Angular velocity of the sphere just after the collision is
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View Solution
