Question

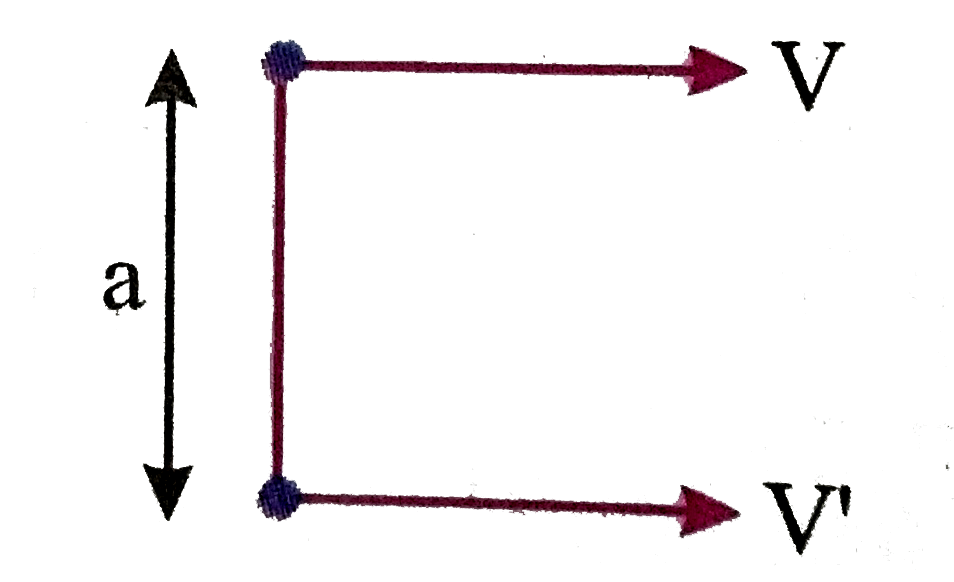
Two particles of mases $m$ and $m\text{'}$ moving on parallel straight lines are at the distance $\text{'}a\text{'}$ apart with velocities $v$ and $v\text{'}(v>v\text{'})$. The particles are connected by a string of length $(>a)$ which was loose in the beginning. Calculate the impluse of tension of the string when it becomes taut.

Answer

`(m m'(v-v')sqrt(l^(2)-a^(2)))/((m+m')l)`

Explanation

Just before string becomes taut

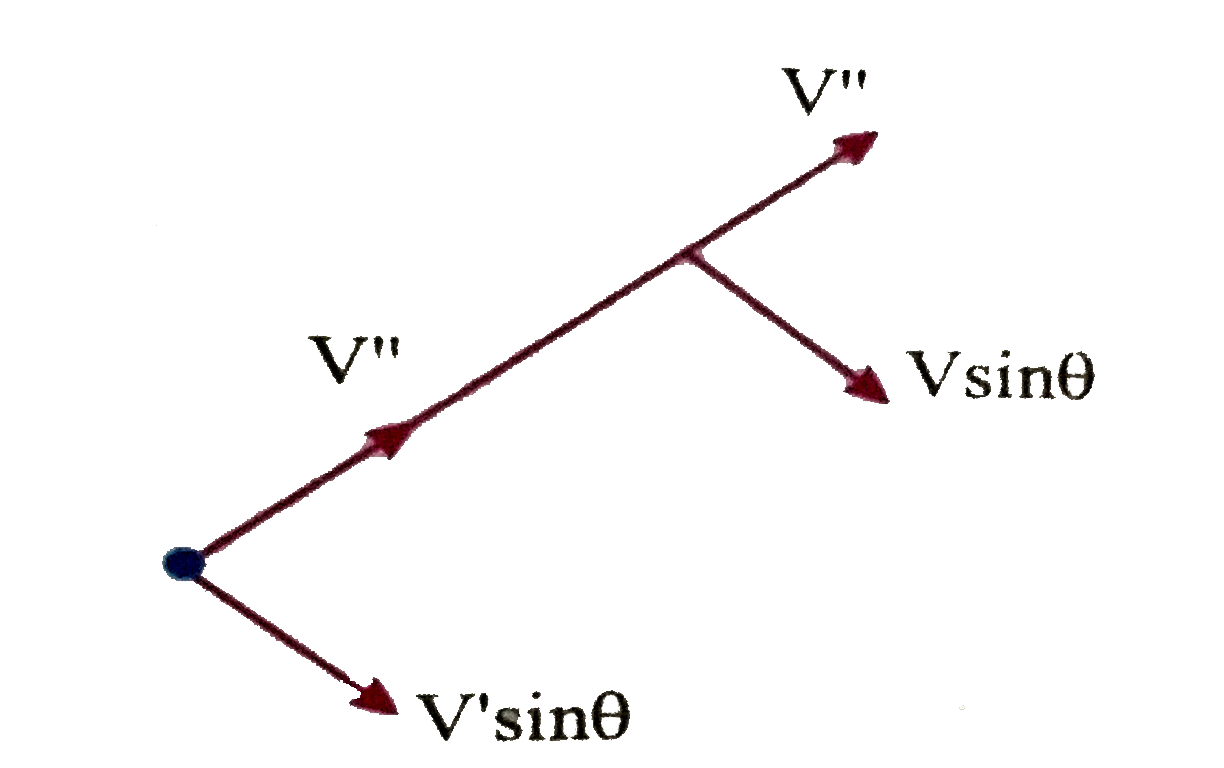
Just after string becomes taut.
`T Delta t = m(V cos theta-V'') , T Delta t = m'(V''-V' cos theta)`
`rArr v'' = ((m v+m'v') cos theta)/((m+m'))`
`T Delta t = J = (m m'(V-V')sqrt(l^(2)-a^(2)))/((m+m')l)`