Stationary particles of mass m2 is hit by another particles of mass m1. The stationary particle deviates through θ and the other by 90∘. Find the value of θ if the collision is perfectly elastic.
The correct Answer is:cosθ=√m1+m22m2
m1u=m2v2cosθFrom COMm1v1=m2v2sinθ⎫⎪⎬⎪⎭ ...(i)

From COE
12m1u2=12m1v21+12m2v22
⇒m1u2=m1v21+m2v22 ...(ii)
From (i) m22v22=m21(u2+v21)
Putting the value of m1v21 in (ii)
m1u2=m22v22−m21u2m1+m2v22
⇒v21u2=m22v22−m21u2+m1m2v22
⇒2m21u2=m2v22(m1+m2)
⇒v22=2m21m2(m1+m2)
Putting in (i)
m1u=
⎷2m21m2(m1+m2)ucosθ⇒1=√2m2m1+m2cosθ
⇒cosθ=√m1+m22m2
Topper's Solved these Questions
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-I (H.W)
Explore 52 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-II (H.W)
Explore 54 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Comprehension type
Explore 35 Videos
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:LEVEL II(H.W)
Explore 51 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
Similar Questions
A particle of mass m1 collides elastically with a stationary particle of mass m2(m1>m2). Find the maximum angle through which the striking particle may deviate as a result of the collision.
View SolutionA particle A with a mass mA is moving with a velocity v and hits a particle B (mass mB) at rest (one dimensional motion). Find the change the de-Broglie wavelength of the particle A. Treat the collision as elastic.
View Solution
Knowledge Check
A particle (A) of mass m1 elastically collides with another stationary particle (B) of mass m2. Then :
Am1m2=12 and the particles fly a part in the opposite direction with equal velocities.Bm1m2=13 and the particles fly apart in the opposite direction with equal velocities.Cm1m2=21 and the collision angle between the particles is 60∘ symmetrically.Dm1m2=21 and the particles fly apart symmetrically at an angle 90∘A particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
A0.8vB0.2vC0.6vD0.4vA particle of mass m moving with velocity v strikes a stationary particle of mass 2m and sticks to it. The speed of the system will be.
Av//2B2 vCv//3D3 v
A particle of mass m strikes another particle of same at rest. Find the angle between velocities of particles after the collision , if the collision is elastic.
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it. The speed of the system will be
View SolutionA uniform thin stick of mass M=24kg and length L rotates on a friction less horizontal plane, with its centre of mass stationary. A particle of mass m is placed on the plane at a distance x=L3 from the centre of the stick . This stick hits the particle elastically
(a) Find the value of m so that after the collision, there is no rotational motion of the stick
(b) For what minimum of x can we get a value of ‘m’ so that the rod has no rotational motion after elastic collision ?
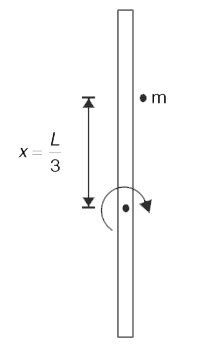
View SolutionA particle of mass m1, hits another particle in rest of mass m2, obliquely, If both the particles after elastic collision moves perpendicular to each other then m1m2 is
View SolutionA particle of mass m moving with a speed v hits elastically another staionary particle of mass 2m on a smooth horizontal circular tube of radius r. Find the time when the next collision will take place?
View Solution