A particle of mass m strikes another particle of same at rest. Find the angle between velocities of particles after the collision , if the collision is elastic.
To solve the problem of finding the angle between the velocities of two particles after an elastic collision, we can follow these steps:
1. Understand the Problem:
- We have two particles, each with mass m. One particle is moving with an initial velocity v and strikes the second particle, which is at rest.
2. Conservation of Momentum:
- In an elastic collision, both momentum and kinetic energy are conserved. We denote the velocities of the first and second particles after the collision as v1 and v2, respectively.
- The initial momentum of the system is:
Pinitial=mv+0=mv
- The final momentum of the system is:
Pfinal=mv1+mv2
- By conservation of momentum:
mv=mv1+mv2(1)
3. Conservation of Kinetic Energy:
- The initial kinetic energy of the system is:
KEinitial=12mv2
- The final kinetic energy of the system is:
KEfinal=12mv21+12mv22
- By conservation of kinetic energy:
12mv2=12mv21+12mv22(2)
4. Setting Up the Angles:
- Let the angle between the velocity of the first particle after the collision and the original direction of motion be α, and the angle for the second particle be β.
- The momentum vectors can be represented as:
v1=|v1| at angle α
v2=|v2| at angle β
5. Using Vector Components:
- The x-component of momentum before the collision is equal to the x-component after the collision:
mv=mv1cos(α)+mv2cos(β)(3)
- The y-component of momentum before the collision is zero, so:
0=mv1sin(α)−mv2sin(β)(4)
6. Solving the Equations:
- From equation (4), we can express v2sin(β)=v1sin(α).
- Squaring both sides gives:
v22sin2(β)=v21sin2(α)(5)
7. Combining the Results:
- From equations (1) and (2), we can derive relationships between v1 and v2 that will ultimately lead us to the conclusion that:
α+β=90∘
- This is because the cosine of the angle between the two momentum vectors must equal zero, leading to the conclusion that the angles are complementary.
8. Final Result:
- Therefore, the angle between the velocities of the two particles after the collision is:
α+β=90∘
- We have two particles, each with mass m. One particle is moving with an initial velocity v and strikes the second particle, which is at rest.
- In an elastic collision, both momentum and kinetic energy are conserved. We denote the velocities of the first and second particles after the collision as v1 and v2, respectively.
- The initial momentum of the system is:
Pinitial=mv+0=mv
- The final momentum of the system is:
Pfinal=mv1+mv2
- By conservation of momentum:
mv=mv1+mv2(1)
- The initial kinetic energy of the system is:
KEinitial=12mv2
- The final kinetic energy of the system is:
KEfinal=12mv21+12mv22
- By conservation of kinetic energy:
12mv2=12mv21+12mv22(2)
- Let the angle between the velocity of the first particle after the collision and the original direction of motion be α, and the angle for the second particle be β.
- The momentum vectors can be represented as:
v1=|v1| at angle α
v2=|v2| at angle β
- The x-component of momentum before the collision is equal to the x-component after the collision:
mv=mv1cos(α)+mv2cos(β)(3)
- The y-component of momentum before the collision is zero, so:
0=mv1sin(α)−mv2sin(β)(4)
- From equation (4), we can express v2sin(β)=v1sin(α).
- Squaring both sides gives:
v22sin2(β)=v21sin2(α)(5)
- From equations (1) and (2), we can derive relationships between v1 and v2 that will ultimately lead us to the conclusion that:
α+β=90∘
- This is because the cosine of the angle between the two momentum vectors must equal zero, leading to the conclusion that the angles are complementary.
- Therefore, the angle between the velocities of the two particles after the collision is:
α+β=90∘
Topper's Solved these Questions
Similar Questions
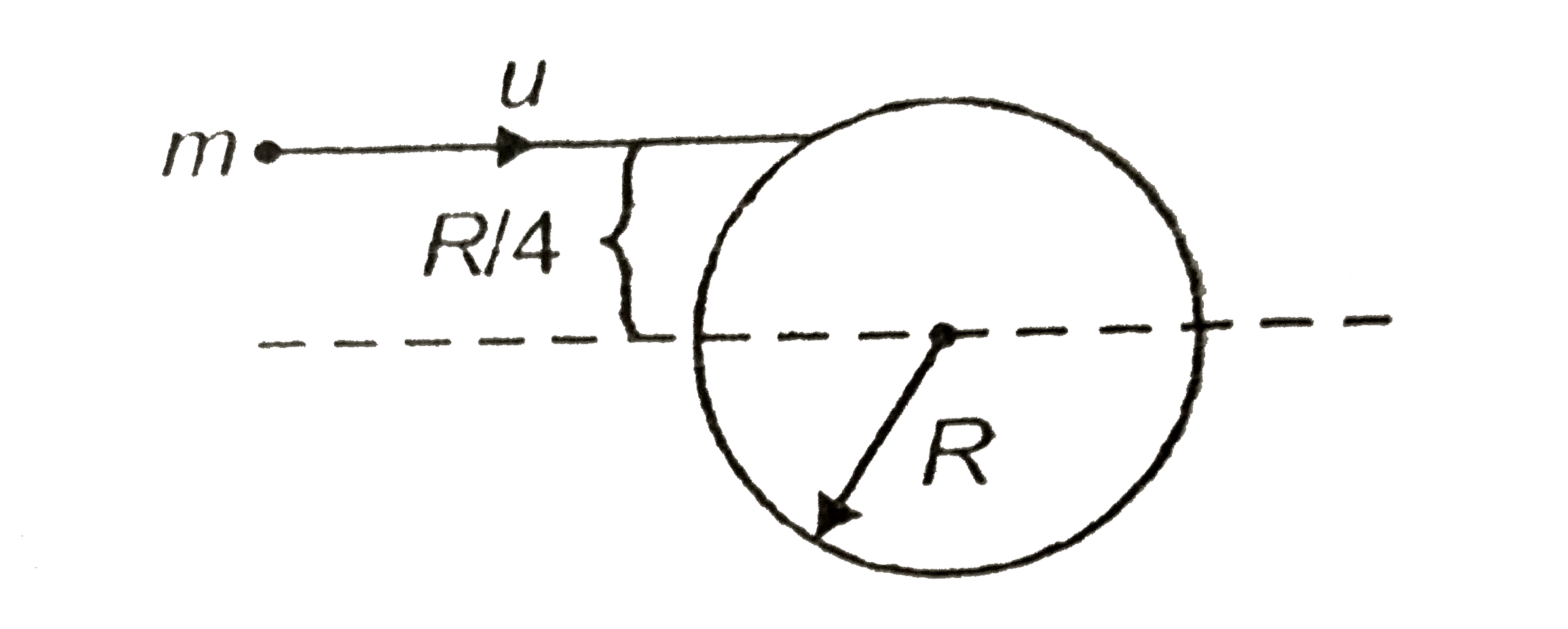
A particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
View SolutionA particle of mass m and veocity →v collides elastically with a stationary particle of mass m Calculate the angle between velocity vector of the two partiicless after the collision.
View Solution
Knowledge Check
A particle of mass m moving with velocity →V makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
A→VB−→VC−2→VDZeroA particle of mass m moving with velocity →V makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
A→VB−→VC−2→VDzeroA particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
A1BmMCM−mM+mDmM+m
A particles of rest mass m0 with kinetic energy T strikes a stationary particle of the same rest mass. Find the rest mass and the velocity of the compound particle formed as a result of the collision.
View SolutionA particle of mass m1 moving on a smooth surface with some velocity strikes another particle of mass m2 at rest. The head - on elastic collision takes place. After the collision , particles move with equal speed in opposite direction . Determine the mass ratio.
View SolutionA particle of mass m1 moves with velocity v1 and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is
View SolutionIn a smooth circular tube of radius R , a particle of mass m moving with speed V0 hits another particle of mass 3m at rest as shown. The time after which the next collision takes place (assume elastic collision)

View SolutionA particle of mass m collides with another stationary particle of mass M such that the second particle starts moving and the first particle stops just after the collision. Then which of the following conditions must always be valid ?
View Solution
