Two particles of mass m and 2 m moving in opposite directions collide elastically with velocities v and 2v. Find their velocities after collision.
0, 3v
1, 3v
0, 1v
0, 4v
The correct Answer is:A
To solve the problem of two particles colliding elastically, we will use the principles of conservation of momentum and conservation of kinetic energy.
Step 1: Define the system
Let:
- Mass of particle 1, m1=m
- Mass of particle 2, m2=2m
- Initial velocity of particle 1, u1=v (moving in the positive direction)
- Initial velocity of particle 2, u2=−2v (moving in the negative direction)
Step 2: Apply conservation of momentum
The total momentum before the collision must equal the total momentum after the collision. The equation for momentum conservation is:
m1u1+m2u2=m1v1+m2v2
Substituting the known values:
m(v)+2m(−2v)=m(v1)+2m(v2)
This simplifies to:
mv−4mv=mv1+2mv2
−3mv=mv1+2mv2(1)
Step 3: Apply conservation of kinetic energy
For an elastic collision, the total kinetic energy before the collision equals the total kinetic energy after the collision:
12m1u21+12m2u22=12m1v21+12m2v22
Substituting the known values:
12m(v2)+12(2m)(−2v)2=12m(v21)+12(2m)(v22)
This simplifies to:
12mv2+12(2m)(4v2)=12mv21+12(2m)v22
12mv2+4mv2=12mv21+mv22
92mv2=12mv21+mv22(2)
Step 4: Solve the equations
From equation (1):
−3=v1+2v2(3)
From equation (2):
9=v21+2v22(4)
Now, we can express v1 in terms of v2 using equation (3):
v1=−3−2v2
Substituting v1 into equation (4):
9=(−3−2v2)2+2v22
Expanding:
9=(9+12v2+4v22)+2v22
Combining like terms:
9=9+12v2+6v22
Subtracting 9 from both sides:
0=12v2+6v22
Factoring out 6v2:
0=6v2(2+v2)
This gives us two solutions:
1. v2=0
2. v2=−2
Step 5: Find v1
Using v2=−2:
Substituting back into equation (3):
v1=−3−2(−2)=−3+4=1
Final Velocities
Thus, the final velocities after the collision are:
- v1=1
- v2=−2
Summary
The final velocities of the two particles after the elastic collision are:
- Particle of mass m has a velocity of 1.
- Particle of mass 2m has a velocity of −2.
Let:
- Mass of particle 1, m1=m
- Mass of particle 2, m2=2m
- Initial velocity of particle 1, u1=v (moving in the positive direction)
- Initial velocity of particle 2, u2=−2v (moving in the negative direction)
The total momentum before the collision must equal the total momentum after the collision. The equation for momentum conservation is:
For an elastic collision, the total kinetic energy before the collision equals the total kinetic energy after the collision:
From equation (1):
2. v2=−2
Using v2=−2:
Thus, the final velocities after the collision are:
- v2=−2
The final velocities of the two particles after the elastic collision are:
- Particle of mass m has a velocity of 1.
- Particle of mass 2m has a velocity of −2.
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 141videos
FORCE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)19videos
FORCE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - MHT CET Corner29videos
ELECTROSTATICS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FRICTION IN SOLID AND LIQUIDSEXERCISE - EXERCISE 2 (Miscellaneous Problems)24videos
FRICTION IN SOLID AND LIQUIDS
Similar Questions
Two balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionTwo particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A stationary partical explodes into two partical of a masses m1andm2 which move in opposite direction with velocities v1andv2. The ratio of their kinetic energies E1/E2 is
Am1/m2B1Cm1v2/m2v1Dm2/m1 - Question 2 - Select One
A particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
Av3B−v3C2v3D−2v3 - Question 3 - Select One
A particle of mass m1 moving with velocity v in a positive direction collides elastically with a mass m2 moving in opposite direction also at velocity v. If m2>>m1, then
Athe velocity of m1 immediately after collision is nearly 3vBthe change in momentum of m1 is nearly 4m1vCthe change in kinetic energy of m1 is nearly 4mv2Dall of the above
A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionTwo particles of masses M and 2M, moving as shown, with speeds of 10 m/s and 5 m/s, collide elastically at the origin. After the collision, they move along the indicated diretions with speeds v1 and v2 respectively. The value of v1 and v2 are nearly:
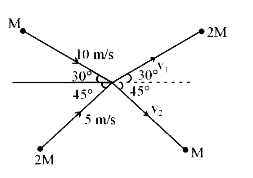 View Solution
View SolutionA ball of mass m moving with velocity v collides elastically with another ball of identical mass coming from the opposite direction with velocity 2v. Their velocities after collisions are-
View SolutionA body of mass 2 kg, travelling at 4 m/s makes a head-on collision with a body of mass 1 kg travelling in the opposite direction with a velocity of 2 m/s, the velocities of the two bodies after collision are
View SolutionTwo masses m, and m, moving with velocities vaandvb in opposite direction collide elastically and after the collision maandmb move with velocities vbandva respectively. Then the ratio mamb is
View Solution

