Consider a sphere of mass 'm' radius 'R' doing pure rolling motion on a rough surface having velocity as shown in the figure. It makes an elastic impact with the smooth wall and moves back and starts rolling after some time again.
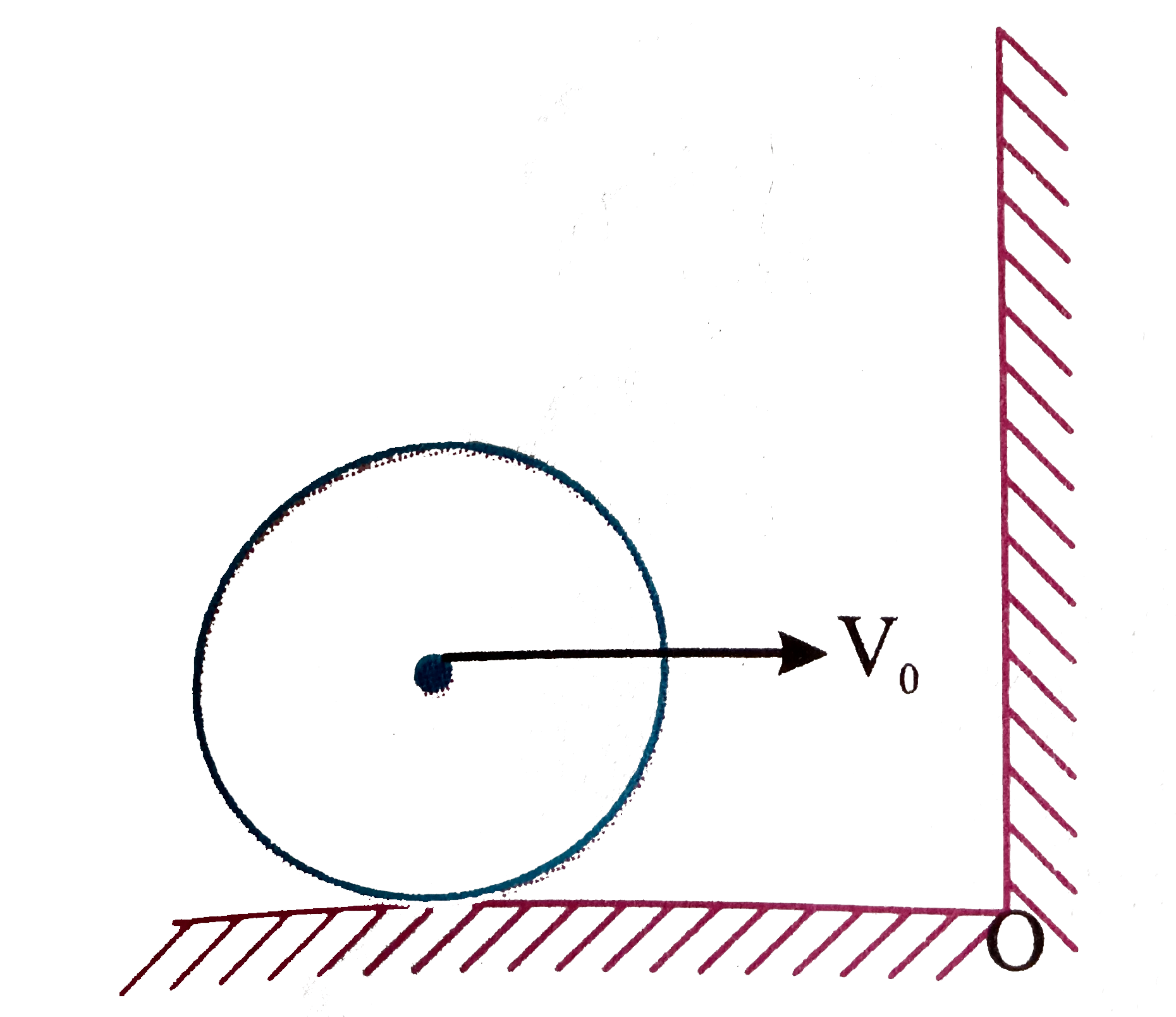
change in angular momentum about in the entire equals in magnitude.
momentum of impulse provided by the wall during impact about equals in magnitude.
final velocity of ball will be
final velocity of ball will be
The correct Answer is:A, B, D
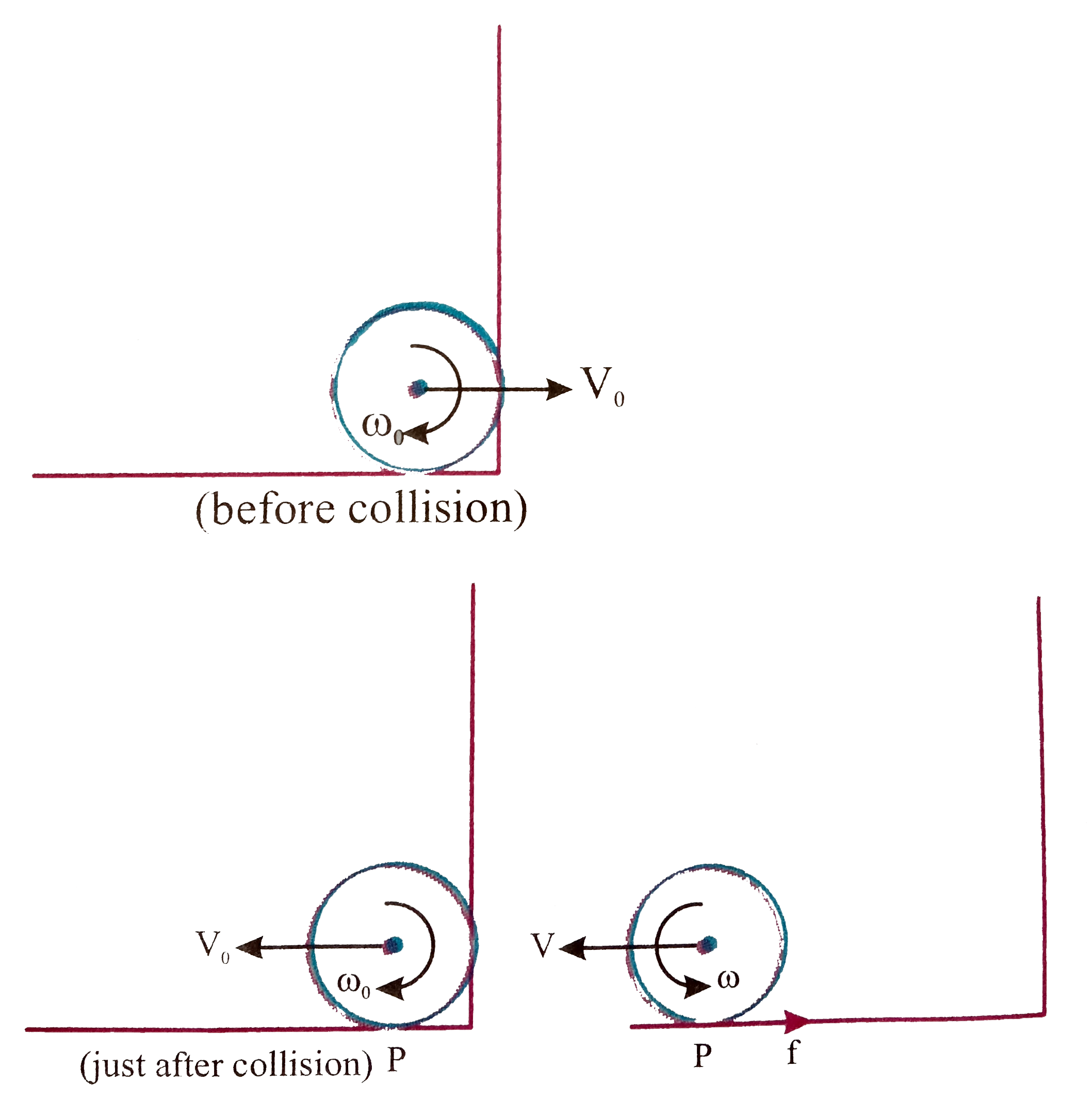 (at the point of pure rolling)
(at the point of pure rolling)
Taking angular momentum about the point
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A rolling body of mass m and radius R is rolling on a rough surface without any pulling force as shown in figure. What happens when it enters on a smooth surface?

View SolutionAn object of mass M and radius R is performing pure rolling motion on a smooth horizontal surface under the action of a constant force F as shown in Fig. The object may be

View Solution
Knowledge Check
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.A solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
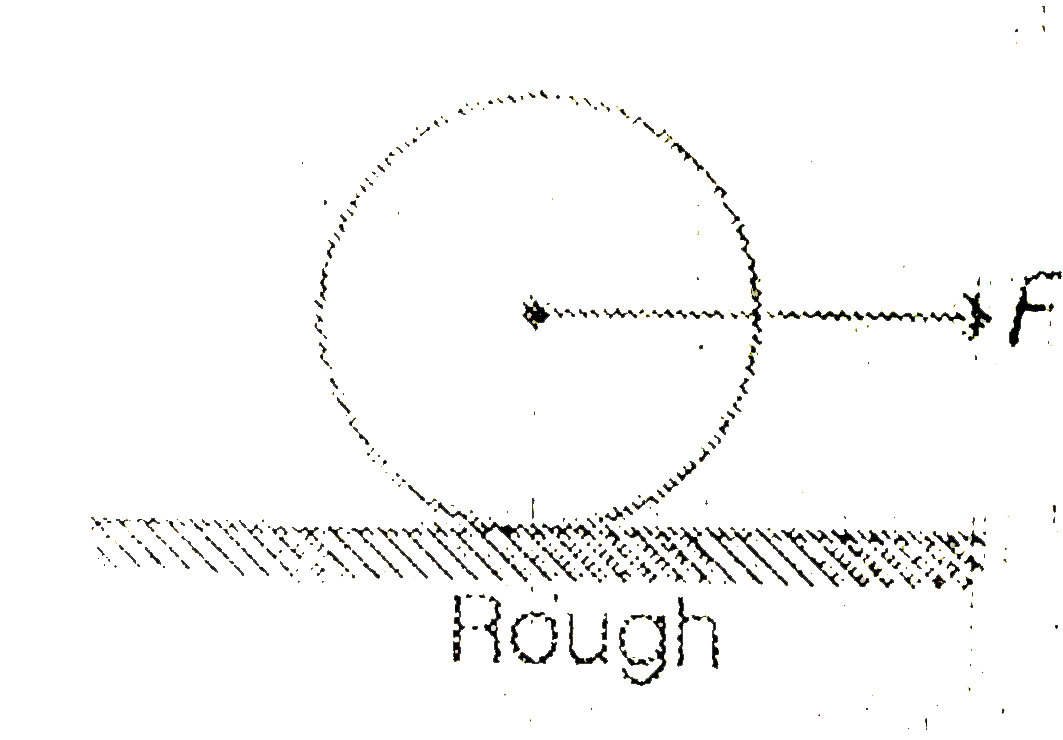 AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3
AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3A uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V0. The kinetic energy of the segment ABC is:
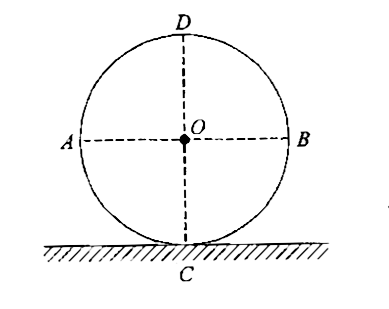 AmV202−mV20πBmv202+mv20πCmv202Dmv20
AmV202−mV20πBmv202+mv20πCmv202Dmv20
A solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
View SolutionA solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
View SolutionA cylinder rolls without slipping on a rough floor, moving with a spped v. It makes an elastic collision with smooth vertical wall. After impact
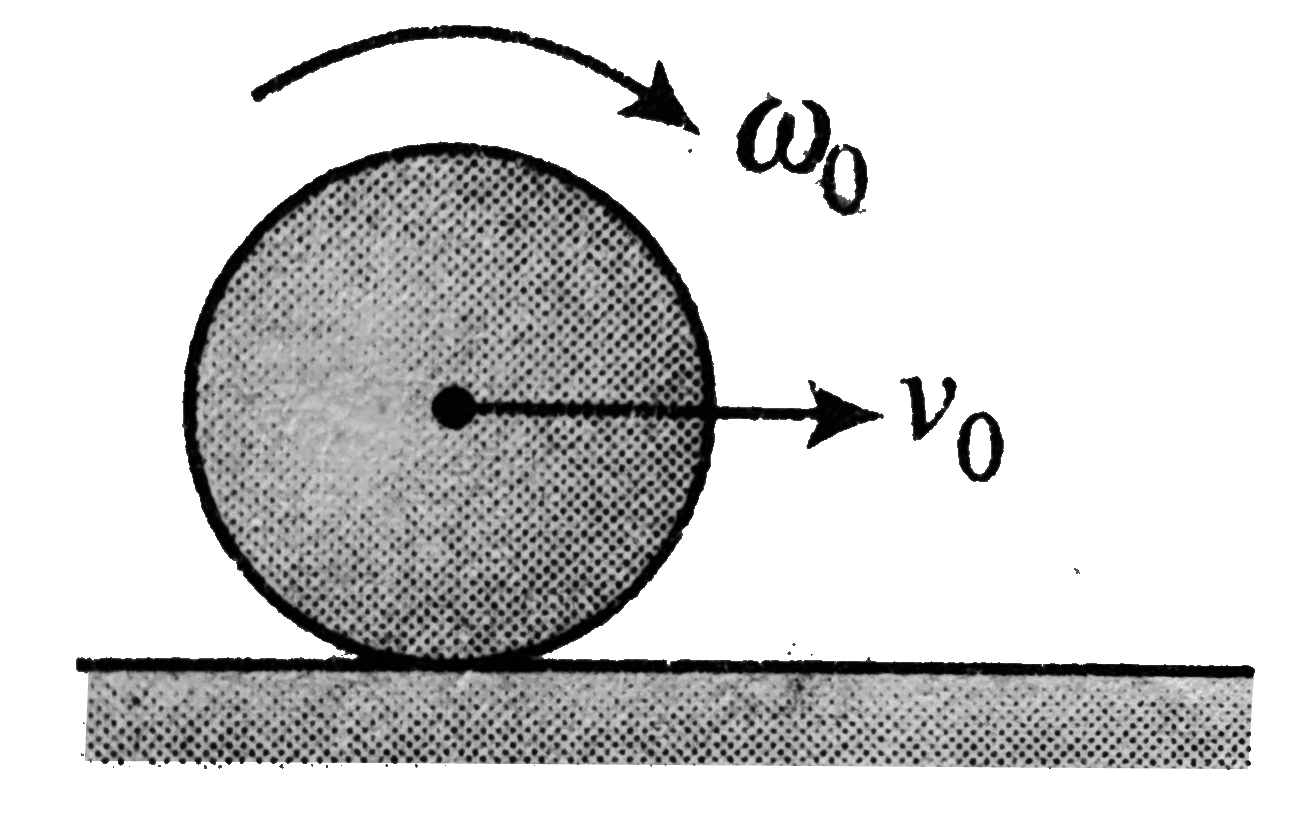
View SolutionA sphere of mass M and radius R is moving on a rough fixed surface, having coefficient of friction μ. as shown in Fig. It will attain a minimum linear velocity after time v0>ω0R)
View SolutionA solid shperical ball of mass m and radius R is present on a rough horizontal surface. A person hit the ball at distance h above the centre of the ball as shown in the figure. Find out the h such that the ball starts pure rolling just after impact.
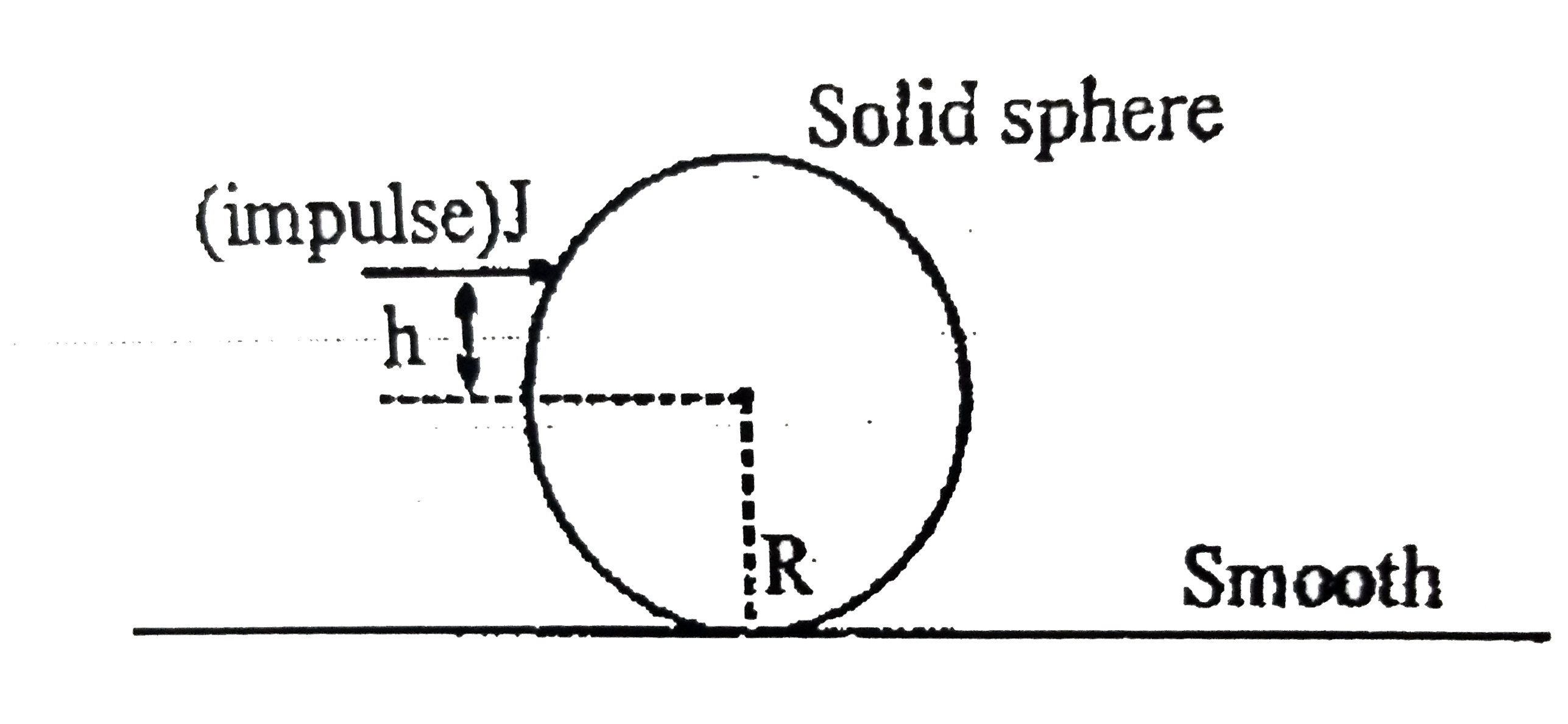
View Solution

