Two vertical walls are separated by a distance of 2 meters, Wall 'A' is smooth while wall B is rough with a coefficient of friction μ=0.5A uniform rod is probed between them. The length of the longest rod that can be probed between the walls is equal to
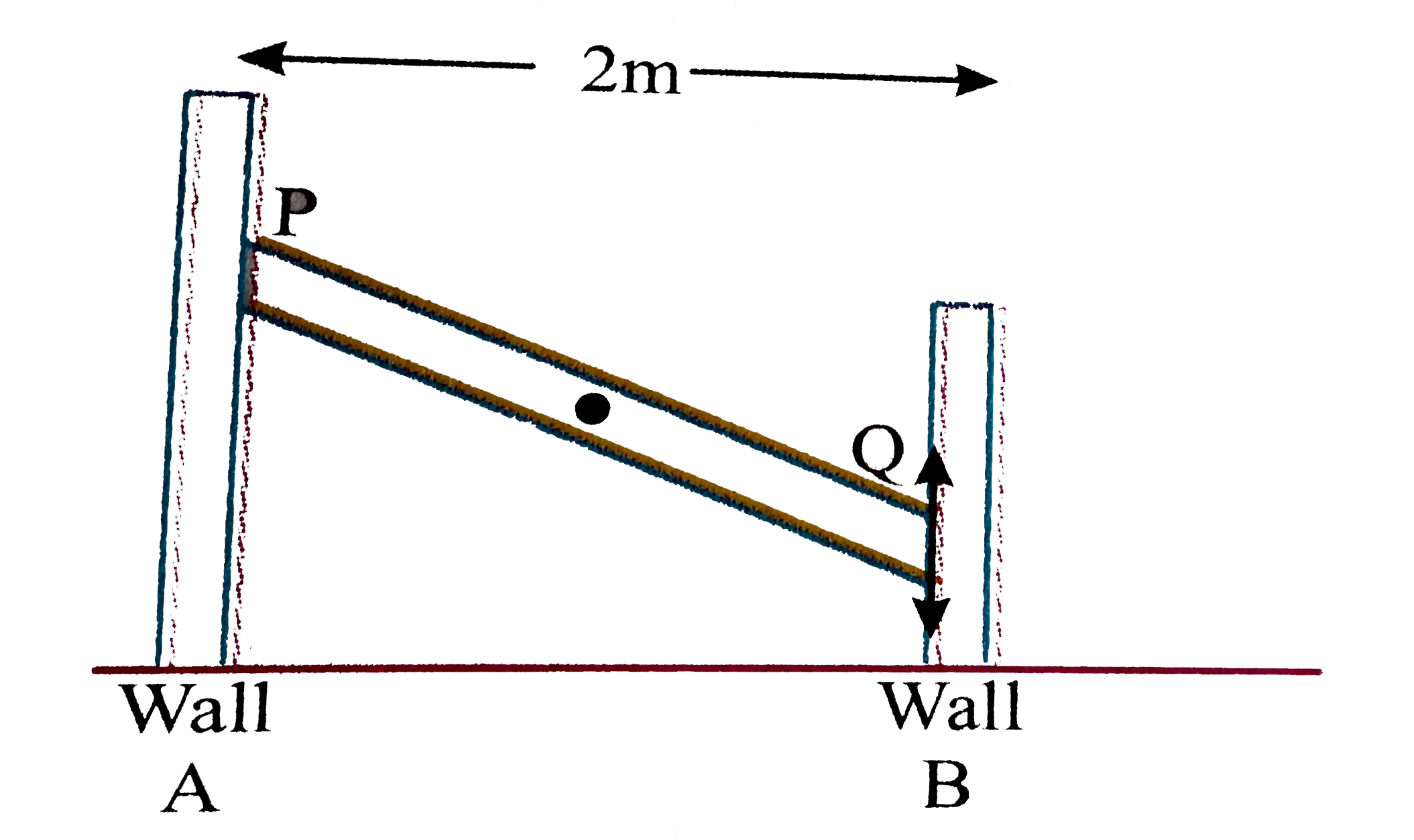
2m
2√2m
√2m
√172m
The correct Answer is:D
μN=mg
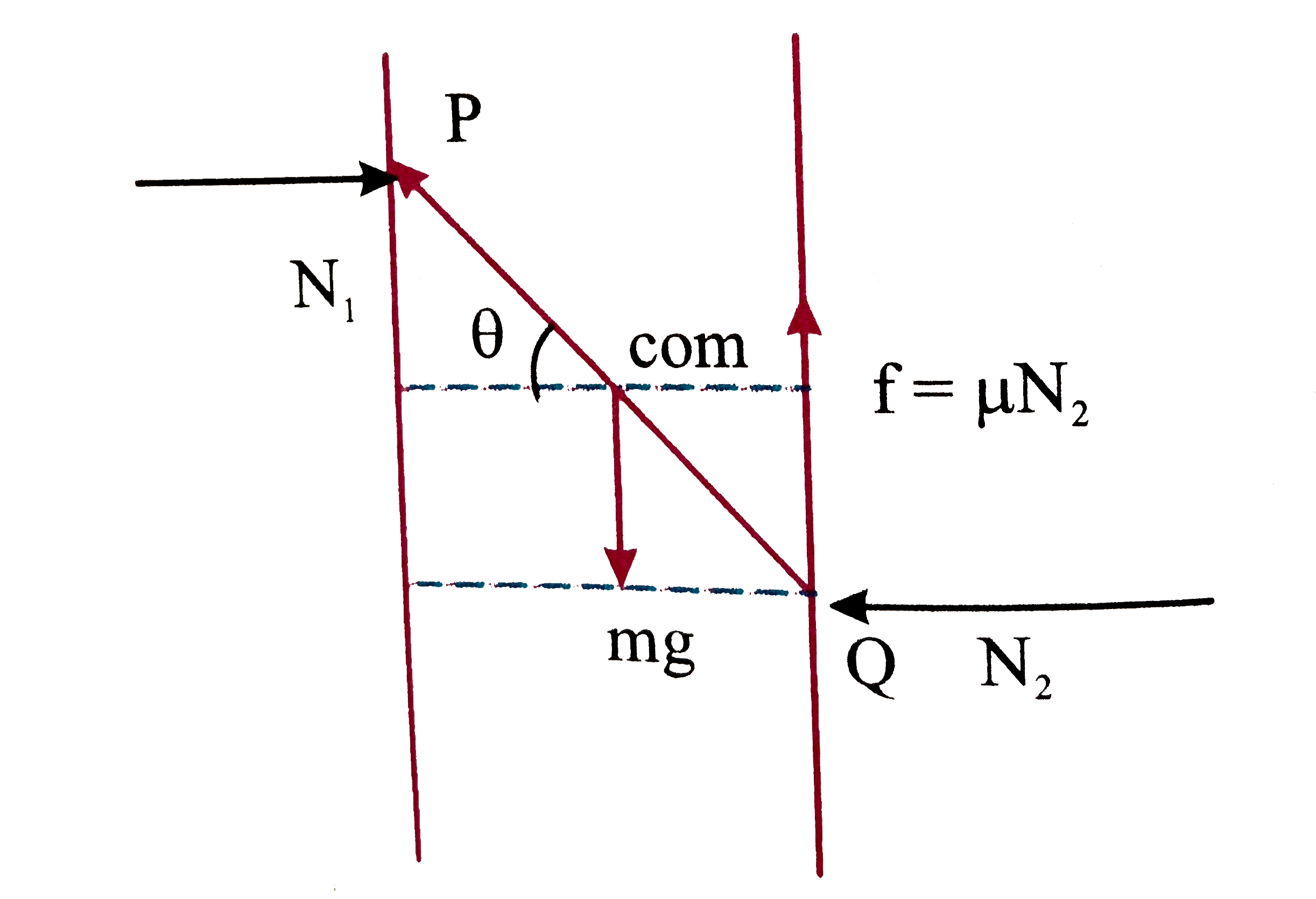
& N1=N2
Take the torque about the com
N112sinθ+N2l2sinθ=μN2l2cosθ
N112sinθ×2=μN2×l2cosθ
tanθ=μ2,√sec2θ−1=12
secθ=√1+l24,l2=√1+0.254,L=√172mt
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A uniform ladder is placed against a wall, if the ground and wall are equally rough the coefficient of friction being tanθ limiting inclination of the ladder to the vertical is 2θ.
View SolutionA uniform rod is made to lean between a rough vertical wall and the ground. The coefficient of friction between the rod and the ground is μ1 and between the rod and the wall is μ2. Find the angle at which the rod can he leaned without slipping.
View Solution
Knowledge Check
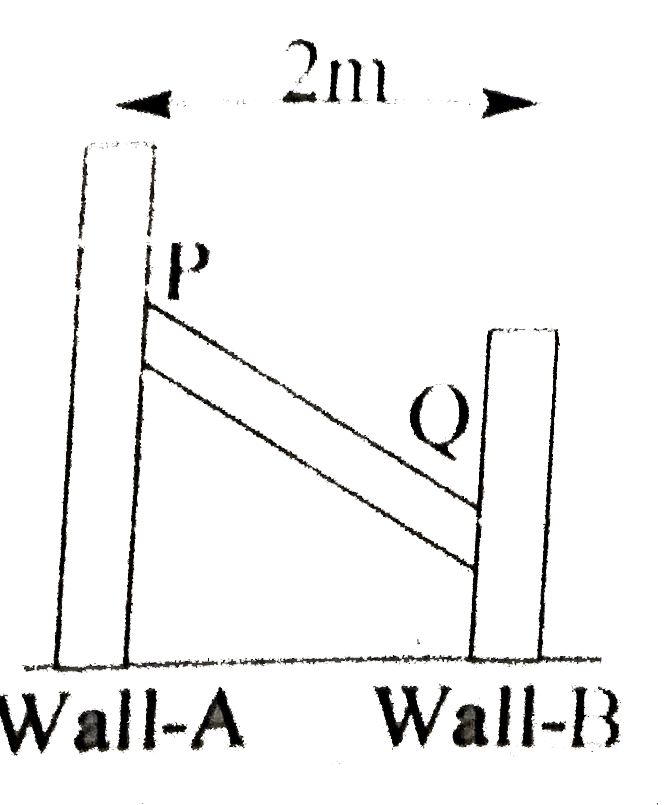
Two vertical walls are separated by a distance of 2 metres. Wall 'A' is smooth while wall B is rough with a coefficient of friction μ=0.5. A uniform rod is propped between them. The length of the longest rod thhat can be probed between te walls is equal toA2 metresB2√2 metresC√5 metresD√172 metresA uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
Atan−1μBcot−1μCcot−1(2μ)Dtan−1(2μ)A uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
Atan−1μBcot−1μCcot−1(2μ)Dtan−1(2μ)
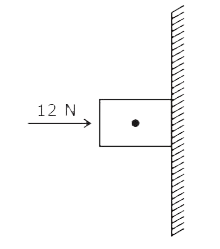
A block of weight 5N is pushed against a vertical wall by a force 12 N. The coefficient of friction between the wall and block is 0.6. The magnitude of the force exerted by the wall on the block is
View SolutionBall A is about to hit a wall at an angle of incidence of θ=30∘. But before hitting the wall it made a head on collision with another identical ball B. The ball B then collides with the wall. The coefficient of restitution for collision between two balls is e1=0.8 and that between a ball and the wall is e1=0.6. Find the final velocity of ball B. Initial velocity of A was u=5ms−1. Neglect friction.
[tan−1(2.252.34)=44∘]
View SolutionA ladder, 10 metre long rests with one end against a smooth vertical wall and the other end on the ground which is rough, the coefficient of friction being 12. The foot of the ladder being 2 metre from the wall. A amn whose weight is 4 times that of the ladder can ascend before it be givens to slip is
View SolutionA ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
View SolutionA sphere is rotatiing between a a rough wall and a smooth wedge as shown in figure If μ is the cofficent of frication between wall and sphere then normal reation between wall and sphere will
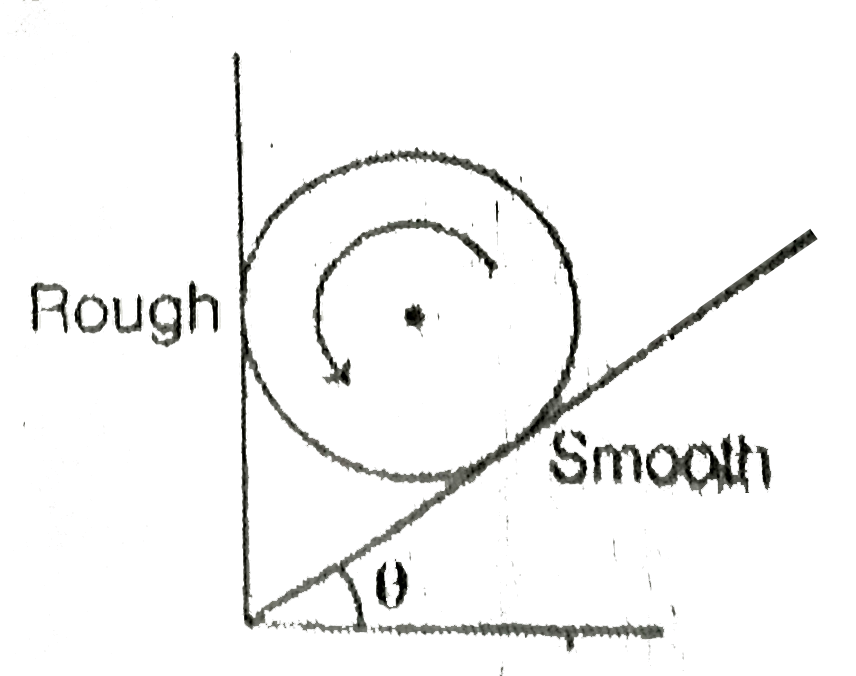
View Solution

