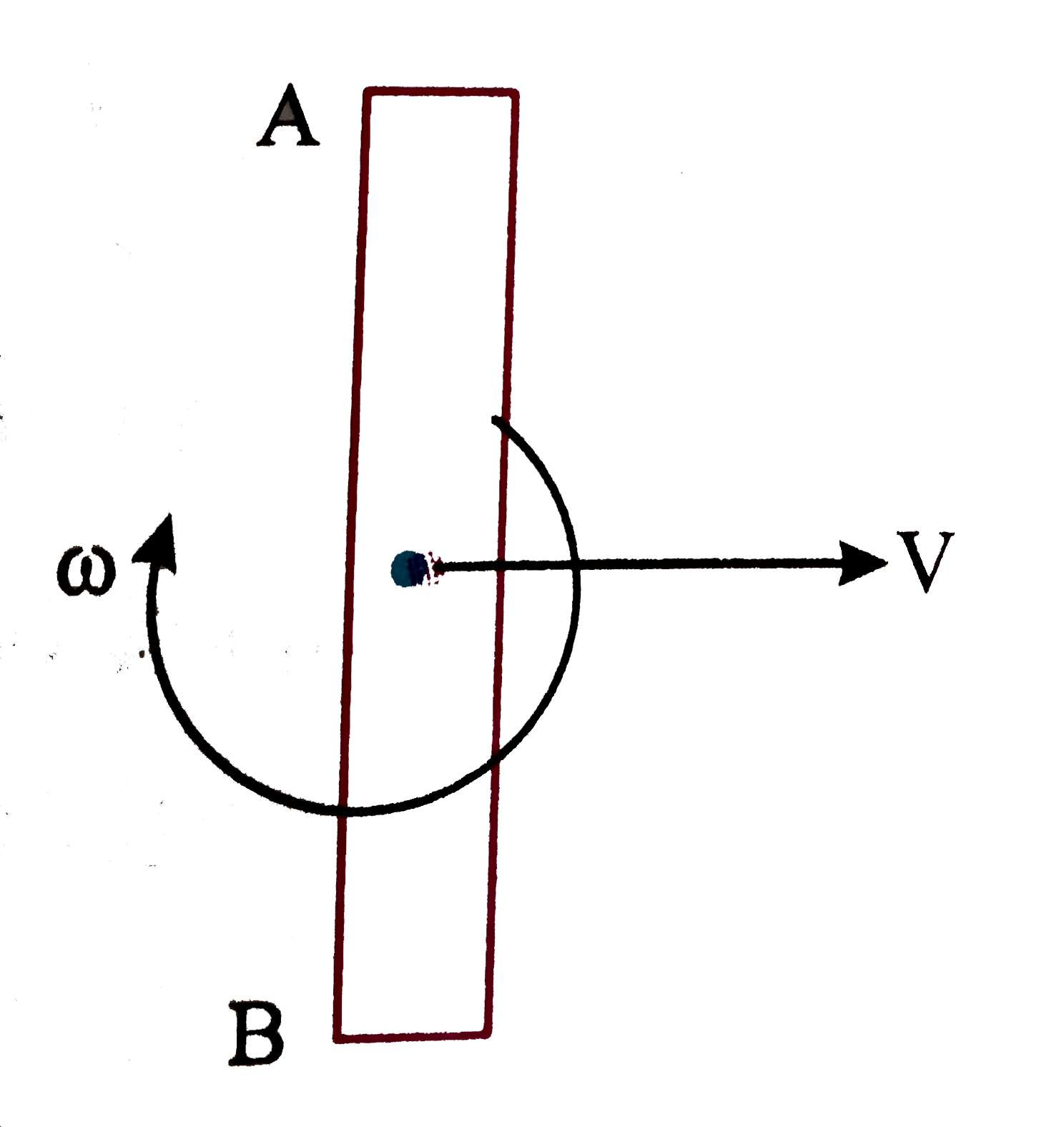
A rod of length l is travelling with velocity v and rotating with angular velocity ω such that ωl2=v. The distance travelled by end B of the rod when rod rotates by an angle π2 is
√2(2)l
52l
3l
4l
The correct Answer is:A
Here the point B if following a curvilinear path whose velocity at any instant is given by vector sum of →V and →ω×→L2. When rod rotates by an angle θ, the situation is as shown in the figure. The speed of end point at this instant is
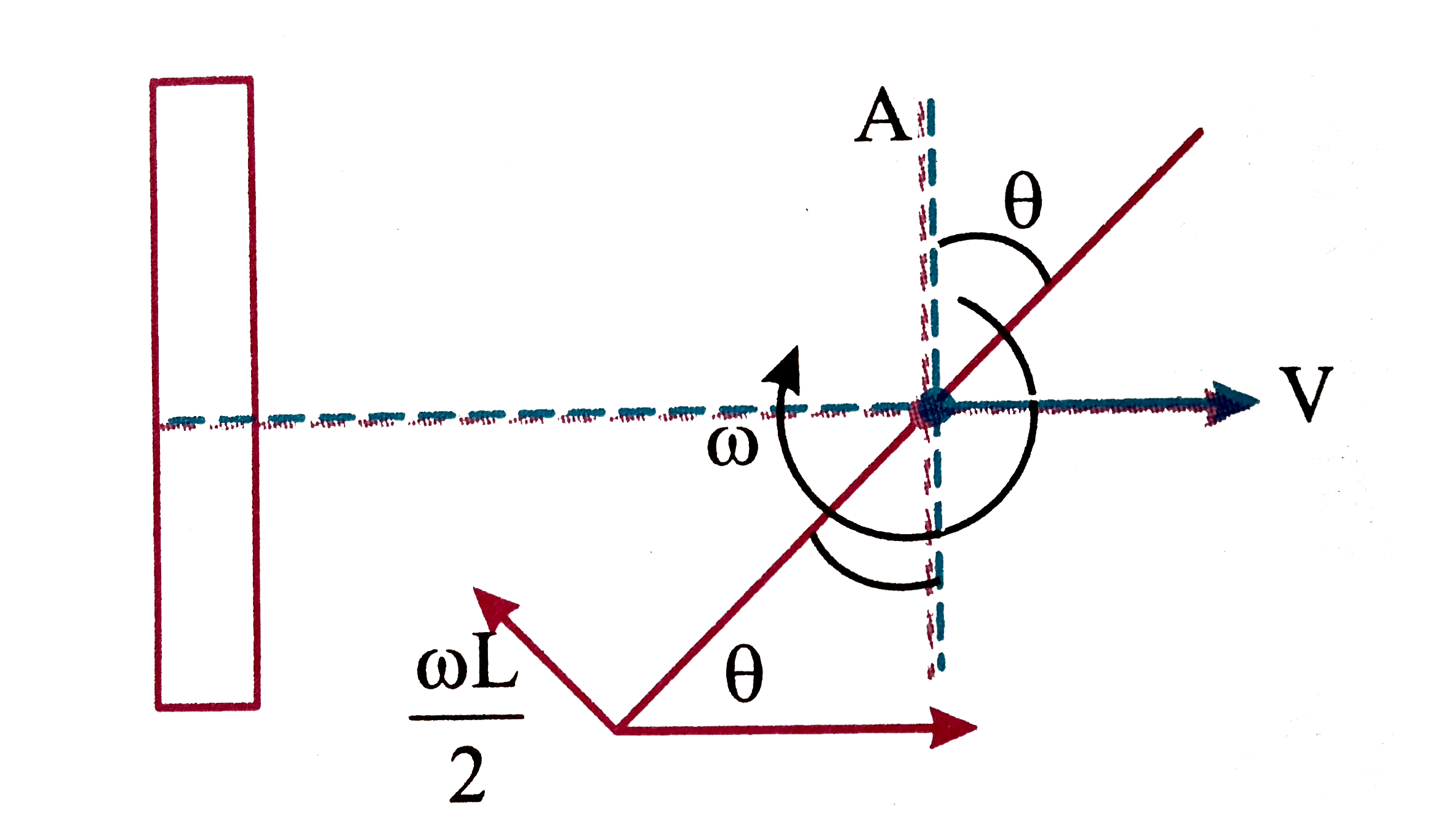
v1=√v2+(ωL2)2+2v+ωL2×cos(π−θ)
v1=√2v(√[1+cosθ])
=√2v×√2cosθ2=2vcosθ2
v1=ωL2×2cosθ2,dsdt=dθdt×Lcosθ2
=∫s0ds=L∫π/20cosθ2dθ=2L√2=√2L
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.

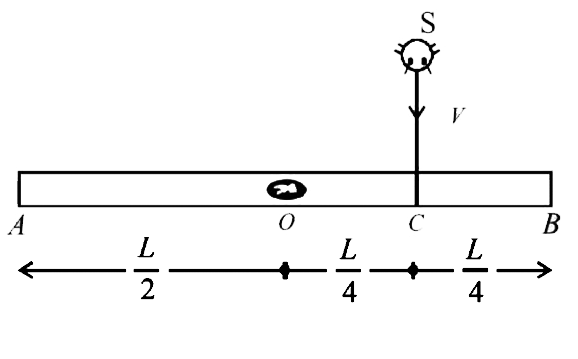
View SolutionA homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
View Solution
Knowledge Check
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
ABωl2B12Bωl2C2Bωl2D14Bωl2A uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.

Distance travelled by the centre of the rod, while rod rotates by 90∘Aπl7Bπl4Cπl12Dπl5
A rod PQ of length l is rotating about end P, with an angular velocity ω. Due to electrifugal forceed the free electrons in the rod move toward the end Q and an emf is created. Find the induced emf.

View SolutionA uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical

View SolutionA thin uniform rod of mass 'M' and ength 'L' is rotating about a perpendicular axis passing through its centre with a constant angular velocity 'ω'. Two objects each of mass M3 are attached gently to the two ends of the rod. The rod will now rotate with an angular velocity of
View SolutionA uniform rod of mass m and length l is rotating with constant angular velocity ω about an axis which passes thorugh its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is y. Neglect gravity. The strain at the mid point of the rod is:
View Solution

