Distance of the centre of mass of a solid uniform cone from its vertex is z0. It the radius of its base is R and its height is h then z0 is equal to:
Video Solution
Text Solution
Consider a cone of height 'h' base radius 'R' and density ρ. To find centre of mass of the cone imagine a small element of radius 'r' and thickness 'dx' at a distance 'x' form 'O' . Mass of small element,dm=(πr2)dxρ.
from figure.
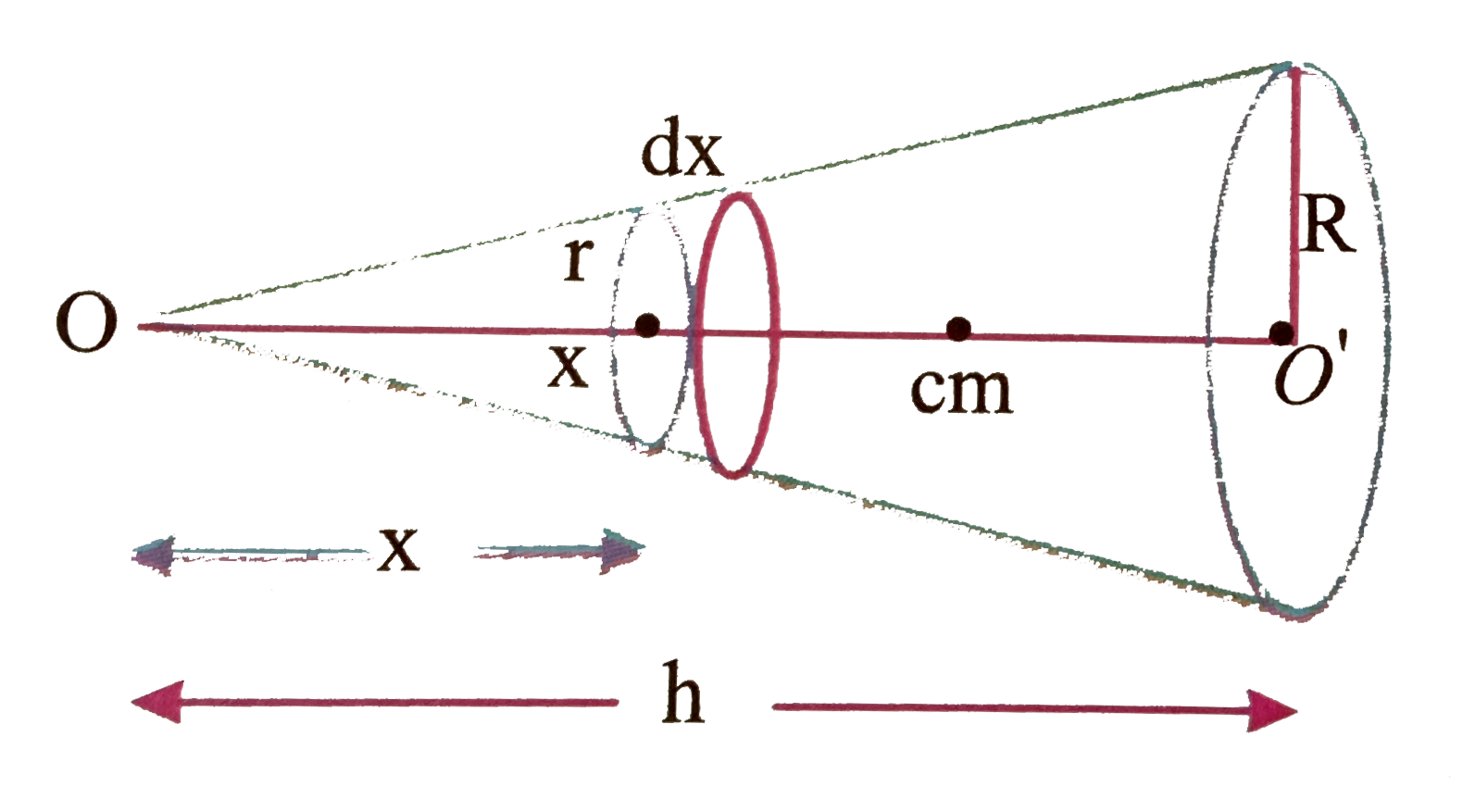
rR=xh⇒r=Rxh
xCM=∫dmx∫dm=∫h0(πr2ρdx)x∫h0πr2dxρ
=∫h0(R2x2h2)xdx∫h0R2x2h2dx=∫h0x3dx∫h0x2dx=(x44)h)(x33)h0=h44h33=3h4
Therefore, centre of mass of cone is at a distance 3h4 from vertex on its line of symmetry.
|
Topper's Solved these Questions
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - C.U.Q.
83 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-1(C.W.)
64 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
Similar Questions
Knowledge Check
Distance of the centre of mass of a solid uniform cone from its vertex is z0 . If the radius of its base is R and its height is h then z0 is equal to:
Ah24RB3h4C5h8D3h28RDistance of the centre of mass of a solid uniform cone from its vertex is z0 . If the radius of its base is R and its height is h then z0 is equal to:
Ab24RB3b4C5h8D3h28RThe distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3
Find the volume of a cone, if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
View SolutionFind the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
View SolutionThe total surface area of a cone is 704 cm2 and the radius of its base is 7 cm . Find its slant height .
View SolutionThe centre of mass of a solid cone along the line form the center of the base to the vertex is at
View SolutionThe radius of a circular cone is R and its height is H. The volume of cone is :
View Solution