The centre of mass of a solid cone along the line form the center of the base to the vertex is at
One-fourth of the height
One-third of the height
One-fifth of the height
None of these
The correct Answer is:A
To find the center of mass of a solid cone along the line from the center of the base to the vertex, we can follow these steps:
Step 1: Understand the Geometry of the Cone
- A solid cone has a circular base and a vertex. Let the radius of the base be R and the height of the cone be H.
Step 2: Set Up the Coordinate System
- Place the cone in a coordinate system such that the vertex is at the origin (0,0) and the base is at height H along the y-axis.
Step 3: Consider a Differential Element
- To find the center of mass, consider a thin disk of thickness dy at a height y from the vertex. The radius of this disk can be expressed in terms of y.
Step 4: Relate the Radius of the Disk to the Height
- Using similar triangles, the radius r of the disk at height y can be expressed as:
r=RHy
Step 5: Calculate the Volume of the Differential Element
- The volume dV of the thin disk is given by:
dV=πr2dy=π(RHy)2dy=πR2H2y2dy
Step 6: Find the Mass of the Differential Element
- If ρ is the density of the cone, the mass dm of the disk is:
dm=ρdV=ρπR2H2y2dy
Step 7: Calculate the Moment about the Vertex
- The moment of the differential mass about the vertex is given by:
dM=y⋅dm=y⋅ρπR2H2y2dy=ρπR2H2y3dy
Step 8: Integrate to Find Total Mass
- The total mass M of the cone is:
M=∫H0dm=∫H0ρπR2H2y2dy=ρπR2H2(y33)H0=ρπR2H3
Step 9: Integrate to Find the Total Moment
- The total moment Mcm about the vertex is:
Mcm=∫H0dM=∫H0ρπR2H2y3dy=ρπR2H2(y44)H0=ρπR2H34
Step 10: Find the Center of Mass
- The center of mass ycm is given by:
ycm=McmM=ρπR2H34ρπR2H3=3H4
Thus, the center of mass of the solid cone along the line from the center of the base to the vertex is located at H4 from the base.
- A solid cone has a circular base and a vertex. Let the radius of the base be R and the height of the cone be H.
- Place the cone in a coordinate system such that the vertex is at the origin (0,0) and the base is at height H along the y-axis.
- To find the center of mass, consider a thin disk of thickness dy at a height y from the vertex. The radius of this disk can be expressed in terms of y.
- Using similar triangles, the radius r of the disk at height y can be expressed as:
r=RHy
- The volume dV of the thin disk is given by:
dV=πr2dy=π(RHy)2dy=πR2H2y2dy
- If ρ is the density of the cone, the mass dm of the disk is:
dm=ρdV=ρπR2H2y2dy
- The moment of the differential mass about the vertex is given by:
dM=y⋅dm=y⋅ρπR2H2y2dy=ρπR2H2y3dy
- The total mass M of the cone is:
M=∫H0dm=∫H0ρπR2H2y2dy=ρπR2H2(y33)H0=ρπR2H3
- The total moment Mcm about the vertex is:
Mcm=∫H0dM=∫H0ρπR2H2y3dy=ρπR2H2(y44)H0=ρπR2H34
- The center of mass ycm is given by:
ycm=McmM=ρπR2H34ρπR2H3=3H4
Similar Questions
Find the centre of mass of a uniform solid cone.
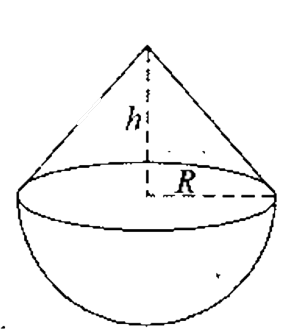
View SolutionA uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown in the figure. The centre of mass of the.composite solid lies at the centre of base of the cone. The height of the cone is √xR. Find x.
'(##CEN_KSR_PHY_JEE_C08_E01_017_Q10##)'
View Solution
Knowledge Check
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is
 A1.5RB√3RC3RD2√3R
A1.5RB√3RC3RD2√3RDistance of the centre of mass of a solid uniform cone from its vertex is z0 . If the radius of its base is R and its height is h then z0 is equal to:
Ab24RB3b4C5h8D3h28RA solid hemisphere and a solid cone have a common base and are made of same material. The centre of mass of the common structure coincides with the centre of the common base. If R is the radius of hemisphere and h is height of the cone, then
 AhR=√3BhR=1√3ChR=3DhR=13
AhR=√3BhR=1√3ChR=3DhR=13
Height the length of the line segment joining the vertex to the center of the base is called the height of the cone.
View SolutionFind the distance of centre of mass of a uniform cone of height 'h' and base radius R, from the vertex on the line of symmetry .
View SolutionA solid of uniform density is made of a hemisphere and a right circular cone which have a common base of radius r . Determine the value of h of the cone if the CG of the system is at the centre of the base.
View SolutionDistance of the centre of mass of a solid uniform cone from its vertex is z0 . If the radius of its base is R and its height is h then z0 is equal to:
View SolutionA uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, so as to have a common face. The centre of mass of the composite solid lies on the common face. The height of the cone is:
View Solution

