Find the distance of centre of mass of a uniform cone of height 'h' and base radius R, from the vertex on the line of symmetry .
To find the distance of the center of mass of a uniform cone from its vertex along the line of symmetry, we can follow these steps:
Step 1: Understand the Geometry of the Cone
We have a uniform cone with height h and base radius R. The vertex of the cone is at the top, and the base is at the bottom.
Step 2: Set Up the Coordinate System
We can set up a coordinate system where the vertex of the cone is at the origin (0,0,0) and the base of the cone is at y=h. The radius of the base at height y can be expressed in terms of y.
Step 3: Relate the Radius and Height
Using similar triangles, we can relate the radius x at a height y to the total height h and the base radius R:
xR=yh⟹x=Rhy
Step 4: Define the Mass Element
Consider a thin disk of thickness dy at height y with radius x. The volume dV of this disk is:
dV=πx2dy=π(Rhy)2dy=πR2h2y2dy
If the density of the cone is ρ, the mass element dm of the disk is:
dm=ρdV=ρπR2h2y2dy
Step 5: Calculate the Center of Mass
The y-coordinate of the center of mass ycm is given by:
ycm=∫ydm∫dm
Substituting for dm:
ycm=∫h0y(ρπR2h2y2dy)∫h0(ρπR2h2y2dy)
Step 6: Evaluate the Integrals
1. Numerator:
∫h0y(ρπR2h2y2dy)=ρπR2h2∫h0y3dy=ρπR2h2(y44)h0=ρπR2h2⋅h44
=ρπR2h24
2. Denominator:
∫h0(ρπR2h2y2dy)=ρπR2h2∫h0y2dy=ρπR2h2(y33)h0=ρπR2h2⋅h33
=ρπR2h3
Step 7: Substitute Back to Find ycm
Now substituting back into the equation for ycm:
ycm=ρπR2h24ρπR2h3=3h4
Conclusion
Thus, the distance of the center of mass from the vertex of the cone along the line of symmetry is:
h4
We have a uniform cone with height h and base radius R. The vertex of the cone is at the top, and the base is at the bottom.
We can set up a coordinate system where the vertex of the cone is at the origin (0,0,0) and the base of the cone is at y=h. The radius of the base at height y can be expressed in terms of y.
Using similar triangles, we can relate the radius x at a height y to the total height h and the base radius R:
xR=yh⟹x=Rhy
Consider a thin disk of thickness dy at height y with radius x. The volume dV of this disk is:
dV=πx2dy=π(Rhy)2dy=πR2h2y2dy
If the density of the cone is ρ, the mass element dm of the disk is:
dm=ρdV=ρπR2h2y2dy
The y-coordinate of the center of mass ycm is given by:
ycm=∫ydm∫dm
Substituting for dm:
ycm=∫h0y(ρπR2h2y2dy)∫h0(ρπR2h2y2dy)
1. Numerator:
∫h0y(ρπR2h2y2dy)=ρπR2h2∫h0y3dy=ρπR2h2(y44)h0=ρπR2h2⋅h44
=ρπR2h24
∫h0(ρπR2h2y2dy)=ρπR2h2∫h0y2dy=ρπR2h2(y33)h0=ρπR2h2⋅h33
=ρπR2h3
Now substituting back into the equation for ycm:
ycm=ρπR2h24ρπR2h3=3h4
Thus, the distance of the center of mass from the vertex of the cone along the line of symmetry is:
h4
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 1
9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 4
11 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
Knowledge Check
The centre of mass of a solid cone along the line form the center of the base to the vertex is at
AOne-fourth of the heightBOne-third of the heightCOne-fifth of the heightDNone of theseFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
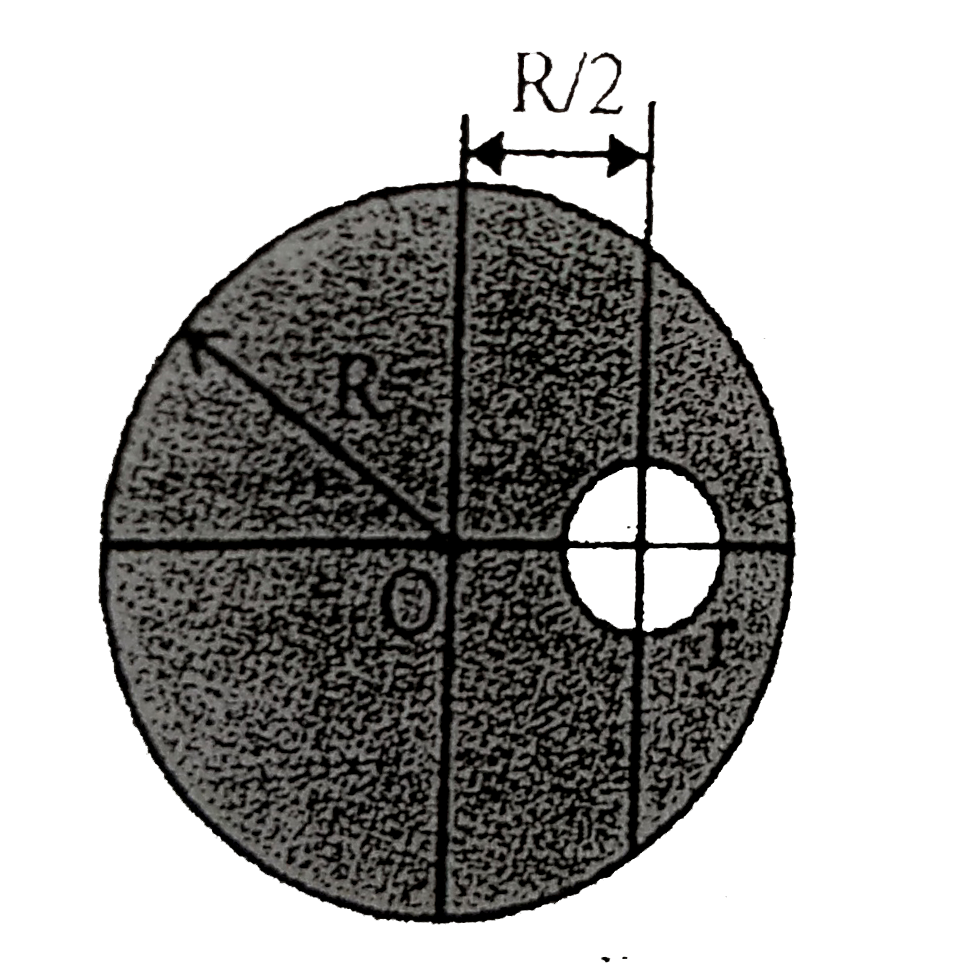 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of OThe distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3
Find the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionDetermine the coordinates of the centre of mass of a right circular soild cone of base radius R and height h.
View SolutionDetermine the coordinate of the centre of mass of a right circular solid cone of base radius R and height h.
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionFind the volume of the cone of height 10 cm and radius of the base 3 cm.
View Solution
