Two blocks of masses 10kg and 30kg are placed on X-axis. The first mass is moved on the axis by a distance of 2cm right. By what distance should the second mass be moved to keep the position of centre of mass unchanged.
To solve the problem, we need to find out how far the second mass (30 kg) should be moved to keep the center of mass of the system unchanged after the first mass (10 kg) is moved 2 cm to the right.
1. Identify the masses and their displacements:
- Let m1=10kg (first mass)
- Let m2=30kg (second mass)
- The first mass is moved d1=2cm to the right.
2. Set up the equation for the center of mass (CM):
The formula for the center of mass R of two masses is given by:
R=m1r1+m2r2m1+m2
where r1 and r2 are the positions of the masses.
3. Initial positions of the masses:
- Assume the initial position of the first mass r1=0 (origin).
- The initial position of the second mass r2=0.
4. Calculate the initial center of mass:
Initially, both masses are at the same position (0), so:
Rinitial=10⋅0+30⋅010+30=0
5. Update the position of the first mass:
After moving the first mass 2 cm to the right, its new position becomes:
r′1=2cm
6. Set the center of mass to remain unchanged:
We want the center of mass to remain at 0 after the first mass is moved. Thus, we set up the equation:
0=10⋅2+30⋅r′210+30
where r′2 is the new position of the second mass after it is moved.
7. Solve for r′2:
Rearranging the equation gives:
0=20+30r′2
30r′2=−20
r′2=−2030=−23cm
8. Interpret the result:
The negative sign indicates that the second mass should be moved 23cm to the left.
Final Answer:
The second mass should be moved 23cm to the left to keep the center of mass unchanged.
- Let m1=10kg (first mass)
- Let m2=30kg (second mass)
- The first mass is moved d1=2cm to the right.
The formula for the center of mass R of two masses is given by:
R=m1r1+m2r2m1+m2
where r1 and r2 are the positions of the masses.
- Assume the initial position of the first mass r1=0 (origin).
- The initial position of the second mass r2=0.
Initially, both masses are at the same position (0), so:
Rinitial=10⋅0+30⋅010+30=0
After moving the first mass 2 cm to the right, its new position becomes:
r′1=2cm
We want the center of mass to remain at 0 after the first mass is moved. Thus, we set up the equation:
0=10⋅2+30⋅r′210+30
where r′2 is the new position of the second mass after it is moved.
Rearranging the equation gives:
0=20+30r′2
30r′2=−20
r′2=−2030=−23cm
The negative sign indicates that the second mass should be moved 23cm to the left.
The second mass should be moved 23cm to the left to keep the center of mass unchanged.
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:C.U.Q.
Explore 83 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-1(C.W.)
Explore 64 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
Two bocks of masses 10 g and 20 kg are placed on the X-axis. The first mass is moved on the axis by a distance of 2 cm. By what distance should the second mass be moved to keep the position of the centre of mass unchanged?
View SolutionTwo blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
View Solution
Knowledge Check
Consider a two-particle system with particles having masses m1andm2 . If the first particle is pushed towards the centre of mass through a distance d, by what distance should the second particle be moved, so as to keep the centre of mass at the same position?
Am2m1dBm1m1+m2dCm1m1dDdConsider a system of two particles having masses 2kg and 5 kg the particle of mass 2 kg is pushed towards the centre of mass of particles through a distance 5 m,by what distance would particle of mass 5kg move so as to keep the centre of mass of particles at the original position?
A2 mB12.5mC8mD5mConsider a two particle system with particles having masses m1andm2 if the first particle is pushed towards the centre of mass through a distance d, by what distance should the second particle is moved, so as to keep the center of mass at the same positon?
Am2m1dBm1m1+m2dCm1m2dDd
Consider a two particle system with the particles having masses m1andm2. If the first particles pushed towards the centre of mass through a distance d, by what distance should the second particle be moved so as the keep the centre of mass at the same position?
View SolutionTwo bodies of masses 3 kg and 4 kg are moving along X axis. At a time t, the bodics are at a distance of 2 m and 3 m from the origin and has velocities of 2ms−1and−3ms−1. Calculate the position and velocity of centre of mass. What will be the total momentum of the system?
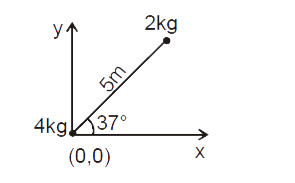
View SolutionTwo particle of mass 4 kg & 2kg are located as shown in figure then find out the position of centre of mass.
View SolutionConsider a system of two particles having masses m1 and m2. If the particle of mass m1 is pushed towards the centre of mass of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the mass centre of particles at the original position?
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View Solution

