Two concentric shells of different mass m1 and m2 are having a sliding particle of mass m. The forces on the sliding at positions I,II and III are respectively

0,Gm1r22,G(m1+m2)mr21
Gm2r22,0,Gm1r21
G(m1+m2)mr21,Gm2r22,0
G(m1+m2)mr21,G(m2)mr22,0
The correct Answer is:D
Position I.F=Gm(m1+m2)r21
(here the particle lies outside of both the shells) position, II. F=Gm2r22. Here the particle lies outside of the shell of mass m1 position III. Here the particle lies inside of both the shell so F=0.
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:NCERT BASED QUESTIONS
Explore 26 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL -I(H.W)
Explore 56 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL II (C.W.)
Explore 38 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
Two concentric shells of masses M1 and M2 are concentric as shown. Calculate the gravitational force on m due to M1 at points P,Q and R.

View SolutionTwo concentric shells of mass m1 and m2 are situated as shown. Find the force on a particle of mass m when the particles is located at (a)r=r1,(b)r=r2,(c)r=r3. The distance r is measured from the centre of the shell.

View Solution
Knowledge Check
Two concentric shells of uniform density of mass M1 and M2 are situated. The forces experienced by a particle of mass m when palced at positions A,B and C respectively are given OA =p,OB = q and OC =r .
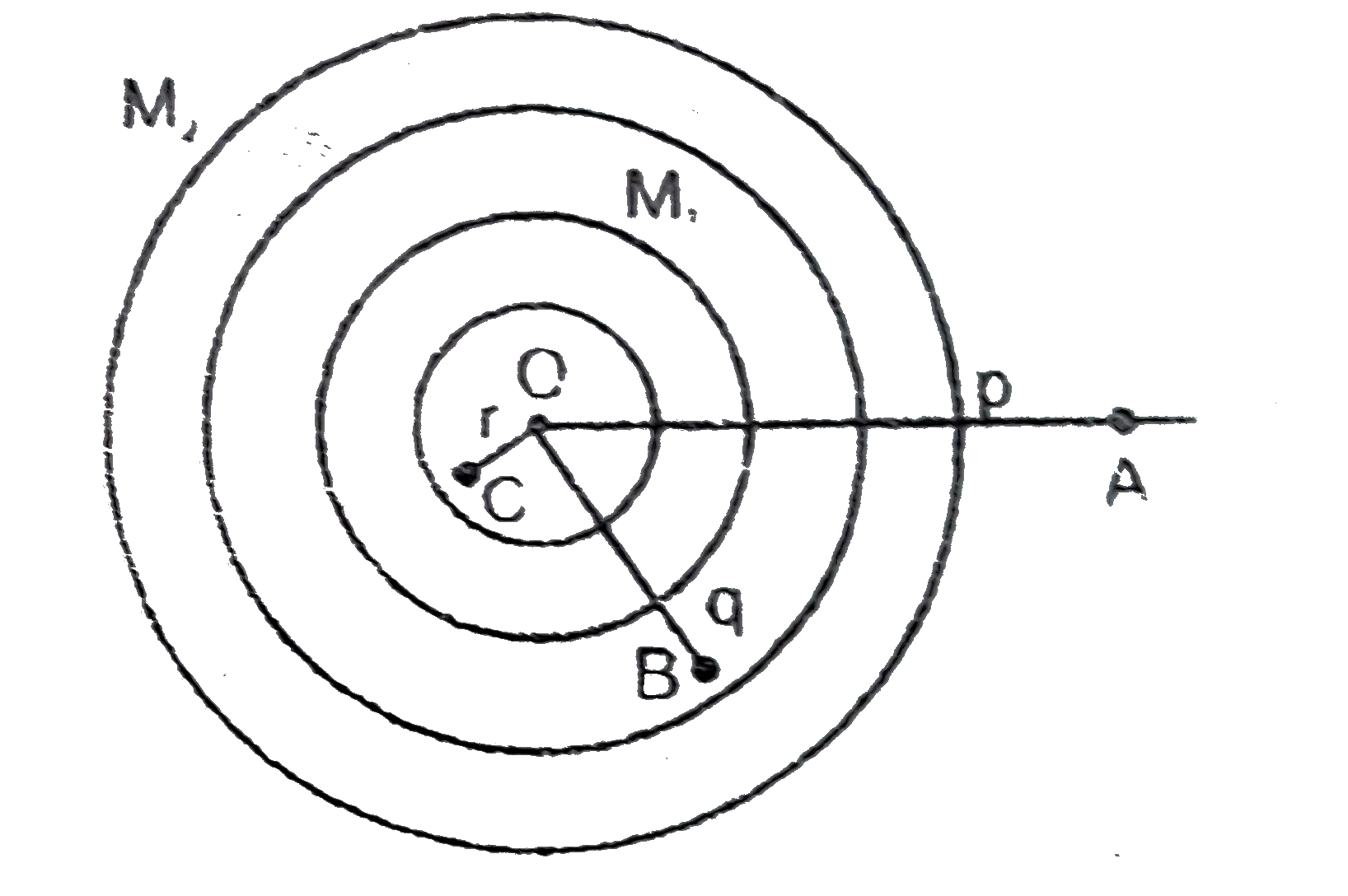 .Azero,GM1mq2and G(M1+m2)mp2BG(m1+M2m)p2andG(M1+m2)mq2andGM1mr2CGM1mq2,GM1mq2 and zeroDG(M1+M2)mp2,GM1mq2 and zero
.Azero,GM1mq2and G(M1+m2)mp2BG(m1+M2m)p2andG(M1+m2)mq2andGM1mr2CGM1mq2,GM1mq2 and zeroDG(M1+M2)mp2,GM1mq2 and zeroTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
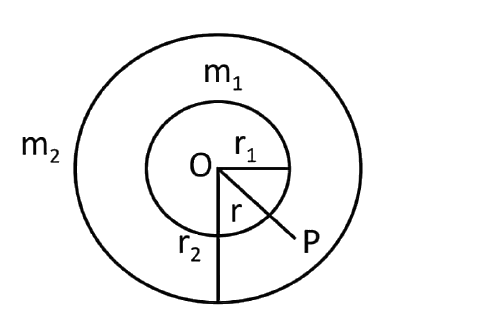
A√m1:√m2Bm1:m2Cm2:m1Dm21:m22Two concentric shells of masses M1 and M2 are having radii r1 and r2. Which of the following is the correct expression for the gravitational field on a mass m?
 AF=G(M1+M2)r2, for r<r1BF=G(M1+M2)(r2), for r<r2CF=GM2r2, for r1<r<r2DF=GM1r2, for r1<r<r2
AF=G(M1+M2)r2, for r<r1BF=G(M1+M2)(r2), for r<r2CF=GM2r2, for r1<r<r2DF=GM1r2, for r1<r<r2
Two concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is
View SolutionTwo particles of mass m1andm2 are in space at separation →r [vector from m(1) to m2]. The only force that the two particles experience is the mutual gravitational pull. The force applied by m1onm2is→F. Prove that μd2→rdt2=→F where μm1m2m1+m2 is known as reduced mass for the two particle system .

View SolutionConsider three concentric shells of masses M1,M2andM3 having radii a,b and c respectively are situated as shown in

Gravitational field at a point located at Q and P is
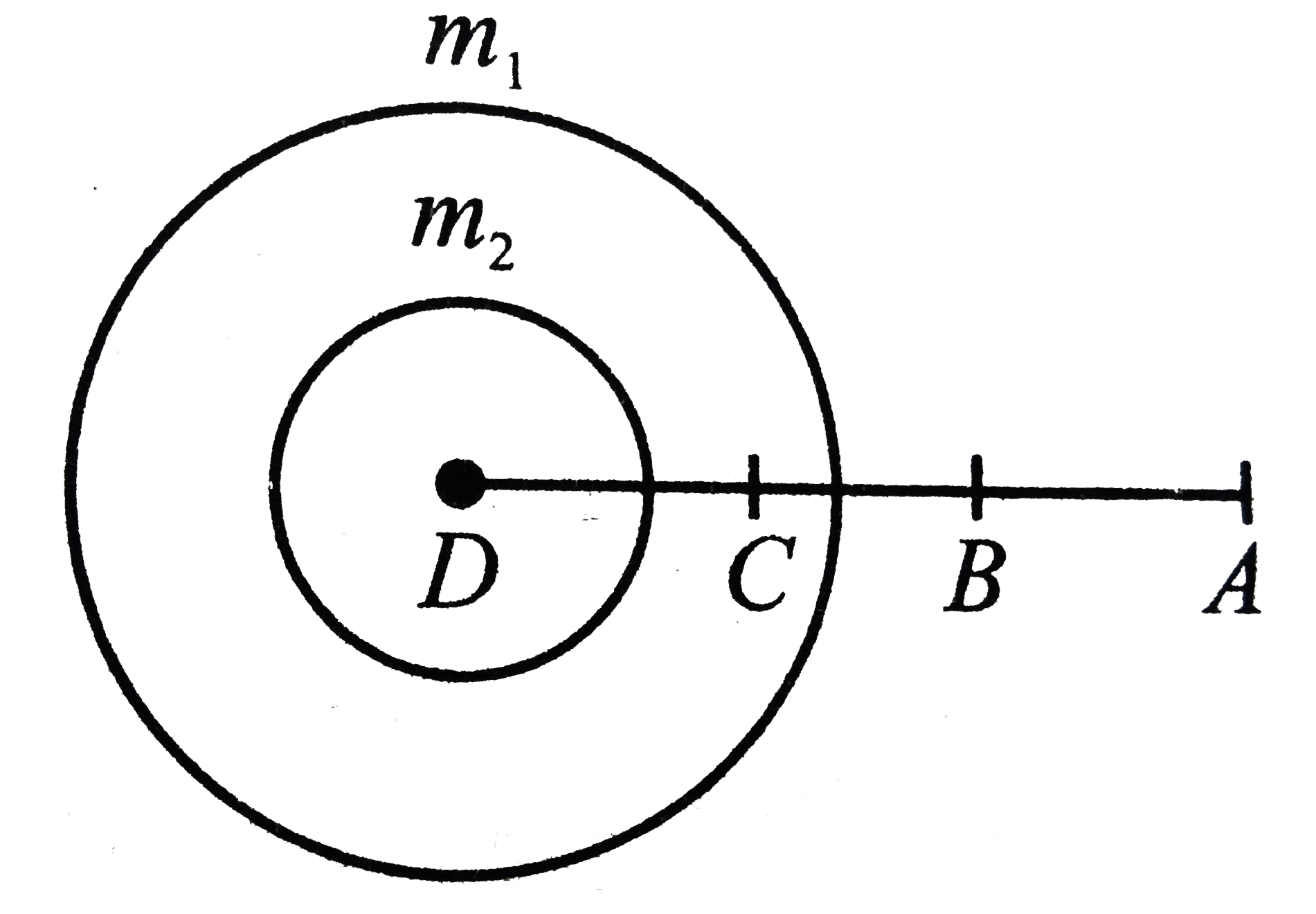
View SolutionFigure shows two shells of masses m1 and m2. The shells are concentric. At which point, a particle of mass m shall experience zero force?
View SolutionA particle (A) of mass m1 elastically collides with another stationary particle (B) of mass m2. Then :
View Solution

