A straight rod of length L extends from x=a to x=L+a. Find the gravitational force exerts on a point mass m at x=0 is (if the linear density of rodμ=A+Bx2)
Gm[Aa+BL]
Gm[A(1a−1a+L)+BL]
Gm[BL+Aa+L]
Gm[BL−Aa]
The correct Answer is:B
To find the gravitational force exerted on a point mass m located at x=0 by a straight rod of length L extending from x=a to x=L+a with a linear density given by μ=A+Bx2, we can follow these steps:
1. Define the setup:
- The rod extends from x=a to x=L+a.
- The point mass m is located at x=0.
- The linear density of the rod is given by μ=A+Bx2.
2. Consider a small element of the rod:
- Let dx be a small element of the rod at position x.
- The mass of this small element dm can be expressed as:
dm=μ⋅dx=(A+Bx2)⋅dx
3. Calculate the gravitational force dF due to the small element:
- The gravitational force exerted by the small mass dm on the point mass m is given by Newton's law of gravitation:
dF=Gmdmr2
- Here, r is the distance from the mass m to the element dx, which is r=x.
- Thus, we have:
dF=Gm(A+Bx2)dxx2
4. Express dF in terms of dx:
- We can separate the terms:
dF=Gm(Ax2+B)dx
5. Integrate to find the total force F:
- The total force F on the mass m is the integral of dF from x=a to x=L+a:
F=∫L+aaGm(Ax2+B)dx
6. Calculate the integral:
- The integral can be split into two parts:
F=Gm(A∫L+aa1x2dx+B∫L+aadx)
- The first integral:
∫1x2dx=−1x
- Evaluating from a to L+a:
∫L+aa1x2dx=−1L+a+1a=1a−1L+a
- The second integral:
∫dx=x
- Evaluating from a to L+a:
∫L+aadx=(L+a)−a=L
7. Combine the results:
- Putting it all together:
F=Gm(A(1a−1L+a)+B⋅L)
Final Expression for the Gravitational Force
F=Gm(A(1a−1L+a)+B⋅L)
- The rod extends from x=a to x=L+a.
- The point mass m is located at x=0.
- The linear density of the rod is given by μ=A+Bx2.
- Let dx be a small element of the rod at position x.
- The mass of this small element dm can be expressed as:
dm=μ⋅dx=(A+Bx2)⋅dx
- The gravitational force exerted by the small mass dm on the point mass m is given by Newton's law of gravitation:
dF=Gmdmr2
- Here, r is the distance from the mass m to the element dx, which is r=x.
- Thus, we have:
dF=Gm(A+Bx2)dxx2
- We can separate the terms:
dF=Gm(Ax2+B)dx
- The total force F on the mass m is the integral of dF from x=a to x=L+a:
F=∫L+aaGm(Ax2+B)dx
- The integral can be split into two parts:
F=Gm(A∫L+aa1x2dx+B∫L+aadx)
- The first integral:
∫1x2dx=−1x
- Evaluating from a to L+a:
∫L+aa1x2dx=−1L+a+1a=1a−1L+a
- The second integral:
∫dx=x
- Evaluating from a to L+a:
∫L+aadx=(L+a)−a=L
- Putting it all together:
F=Gm(A(1a−1L+a)+B⋅L)
F=Gm(A(1a−1L+a)+B⋅L)
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:NCERT BASED QUESTIONS
Explore 26 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL -I(H.W)
Explore 56 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL II (C.W.)
Explore 38 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
A straight of length L extends from x=a to x=L+a. the gravitational force it exerts on a point mass 'm' at x=0, if the mass per unit length of the rod is A+Bx2, is given by :
View SolutionA rod of length l is pivoted about an end . Find the moment of inertia of the rod about this axis if the linear mass density of rod varies as ρ=ax2+b kg/m
View Solution
Knowledge Check
A straight rod of length 'l' extends from x=l to x=2l. If linear mass density of rod is μ=(μ0l3X3), then the gravitational force exerted by rod on a particle of mass m at x=0 , is
A12Gμ0mlBGμ0mlC32Gμ0mlD2Gμ0mlA thin rod of length L is bent to form a semi circle. The mass of the rod is M. What will be the gravitational potential at the centre of the circle?
A−GMLB−GM2πLC−πGM2LD−πGMLA point mass M is at a distance S from an infinitely long and thin rod of linear density D. If G is the gravitational constant then gravitational force between the point mass and the rod is
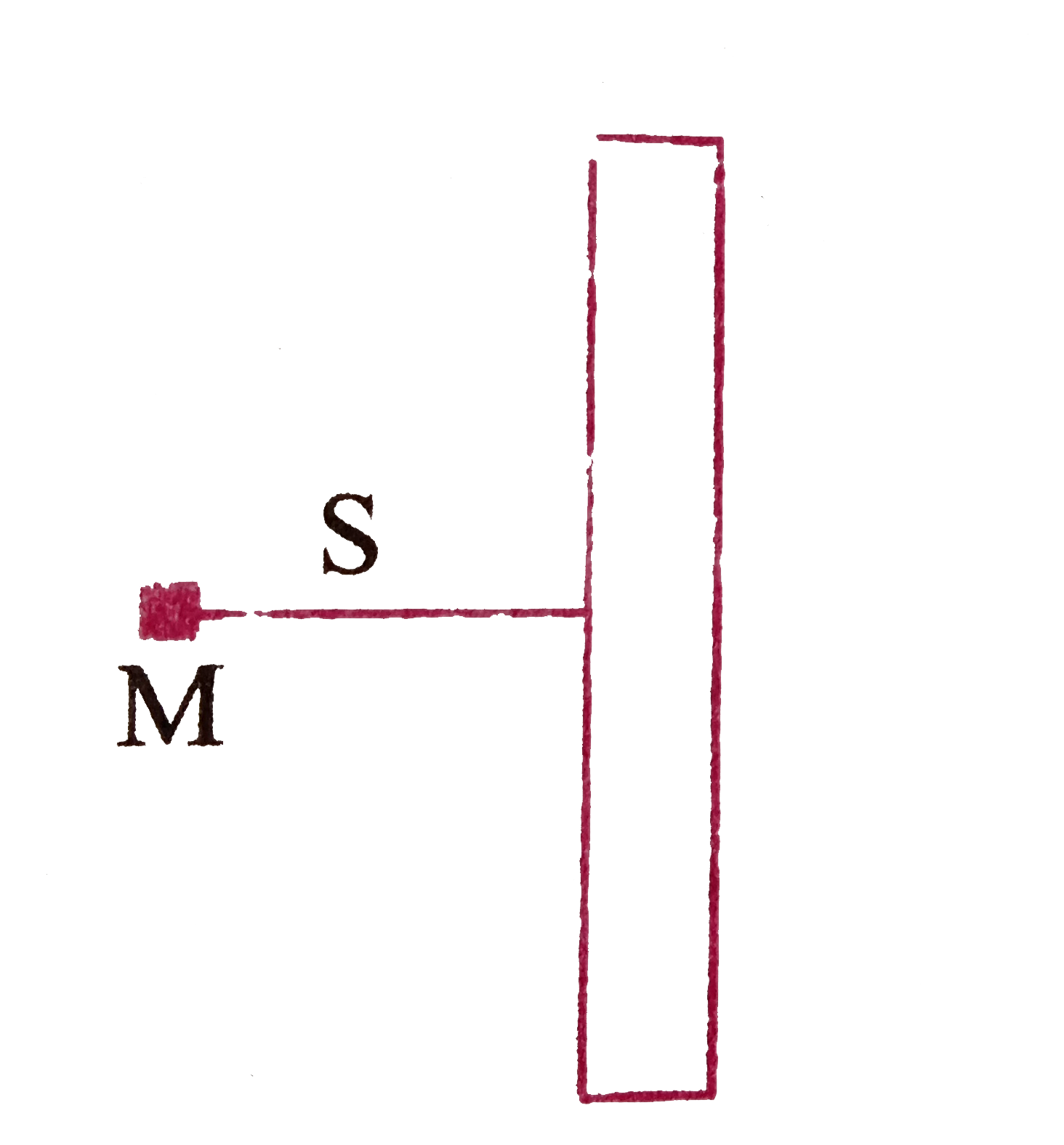 A2GMDSBMGDSCMGD2SD23MGDS
A2GMDSBMGDSCMGD2SD23MGDS
A mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionA thin rod of mass M and length L is bent into a semicircle as shown in diagram. What is a gravitational force on a particle with mass m at the centre of curvature?
View SolutionIf the linear density of a rod of length L varies as λ=A+Bx , find the position of its centre of mass .
View SolutionFind the gravitatinal force of between a point mass m placed at a disance x on the prolongation of a thin rod of mass M andlength l from near end .
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density is λ such that λ=a+bx. Find the mass of the rod.
View Solution

