A rod of length l is pivoted about an end . Find the moment of inertia of the rod about this axis if the linear mass density of rod varies as ρ=ax2+b kg/m
Step by step video & image solution for A rod of length l is pivoted about an end . Find the moment of inertia of the rod about this axis if the linear mass density of rod varies as rho = ax^(2) + b kg/m by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Practice exercise
34 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Discussion Question
30 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
Similar Questions

Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View Solution
Knowledge Check
A rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
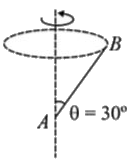 Aml23Bml24Cml216Dml212
Aml23Bml24Cml216Dml212The moment of inertia of a system of four rods each of length l and mass m about the axis shown is
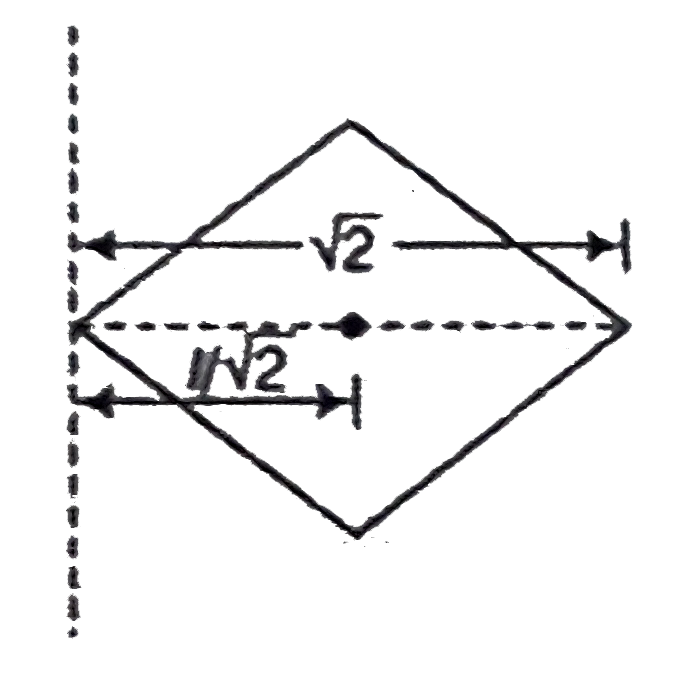 A23ml2B2ml2C3 ml2D83ml2
A23ml2B2ml2C3 ml2D83ml2Mass M is distributed over the rod of length L. If linear mass density (λ) of the rod is linearly increasing with length as l = Kx, where x is measured from one end as shown in figure & K is contant. The moment of inertia. of the rod about the end perpendicular to rod where linear mass density is zero.
AML23BML212C23ML2DKL44
A non-uniform rod AB has a mass M ad length 2l. The mass per unit length of the rod is mx at a point of the rod distant x from A. find the moment of inertia of this rod about an axis perpendicular to the rod (a) through A (b) through the mid-point of AB.
View SolutionA uniform rod of length 1 metre has a mass of 500gram. What is moment of inertia of the rod about an axis passing through the centre of the rod perpendicular to its length. How is moment of inertia changed when the same axis passes through one end of the rod ?
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View SolutionThe moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
View SolutionA thin rod of length l and mass m is turned at mid-point O at angle of 60°. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be

View Solution
