The centres of a ring of mass m and a sphere of mass M of equal radius R, are at a distance √8R apart as shown. The force of attraction between the ring and the sphere is
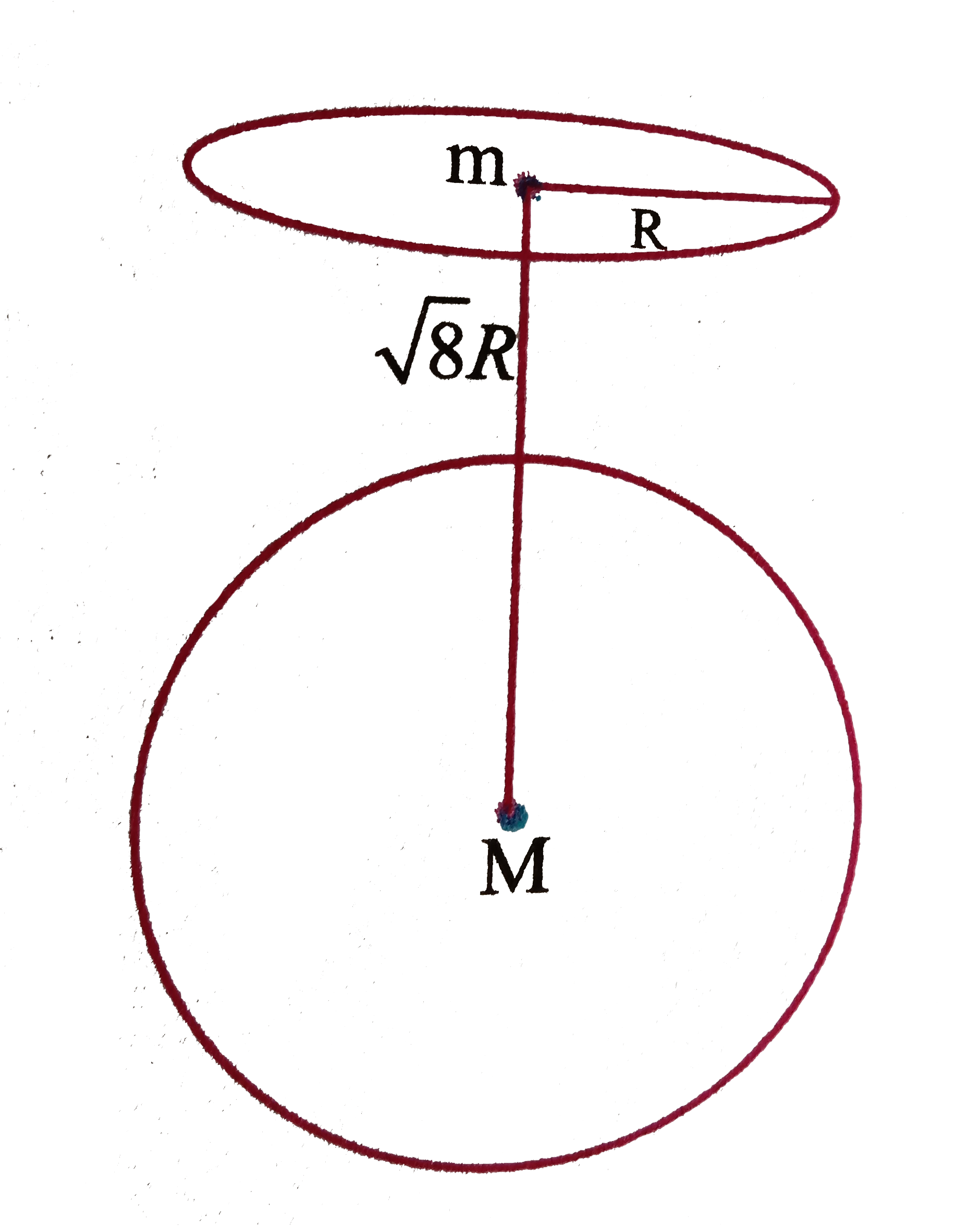
2√227GmMR2
GmM8R2
GmM9R2
√29GmM9R2
The correct Answer is:A
dF=GMdm3R2,F=ΣdFcosθ(or) for a ring, F=GMmx(R2+x2)3/2,x=√8R
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:NCERT BASED QUESTIONS
Explore 26 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL -I(H.W)
Explore 56 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL II (C.W.)
Explore 38 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
A uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
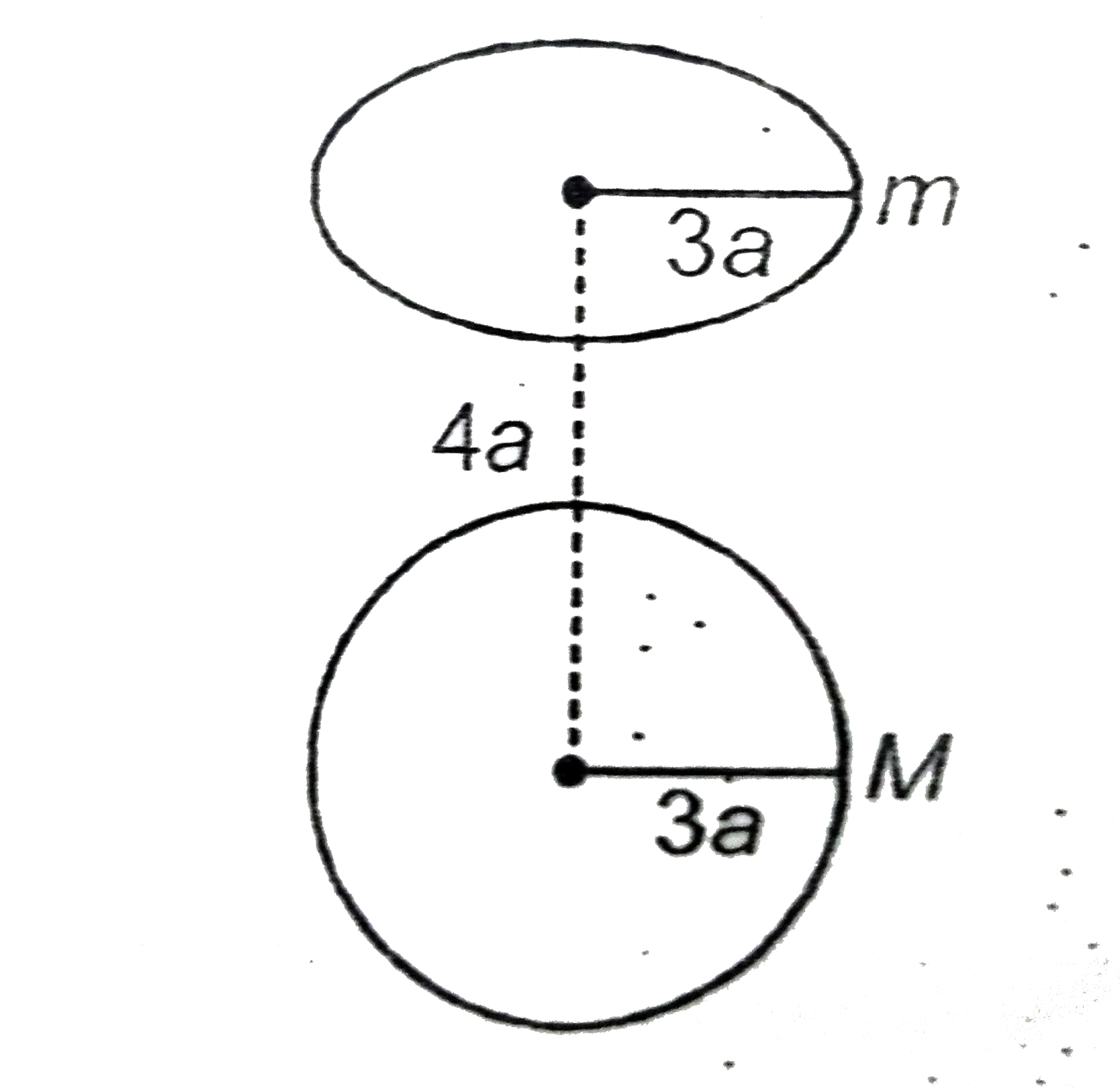
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View Solution
Knowledge Check
Two identical spheres each of mass M and radius R are separated by a distance 3R. The force of attraction between them is proportional to
A1R2BR4CR2D1R4A shell of mass M and radius R has another point mass m placed at a distance r from its centre (r>R). The force of attraction between the shell and point mass is :
AF=GMmrBF=GMmr2Cf=ZeroDNone of theseA particle of mass m lies at a distance r from the centre of earth. The force of attraction between the particle and earth as a function of distance is F(r ),
AF(r)∝1r2 for r<RBF(r)∝1r2 for r≥RCF(r)∝r for r<RDF(r)∝1r for r<R
A particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionThe total energy of rolling ring of mass m and radius R is
View SolutionA particle of mass m is located inside a spherical shell of mass M and radius R. The gravitational force of attraction between them is
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View Solution

