Four masses 'm' each are orbitinting in a circular of radius r in the same direction under gravitational force. Velocityof each particle is
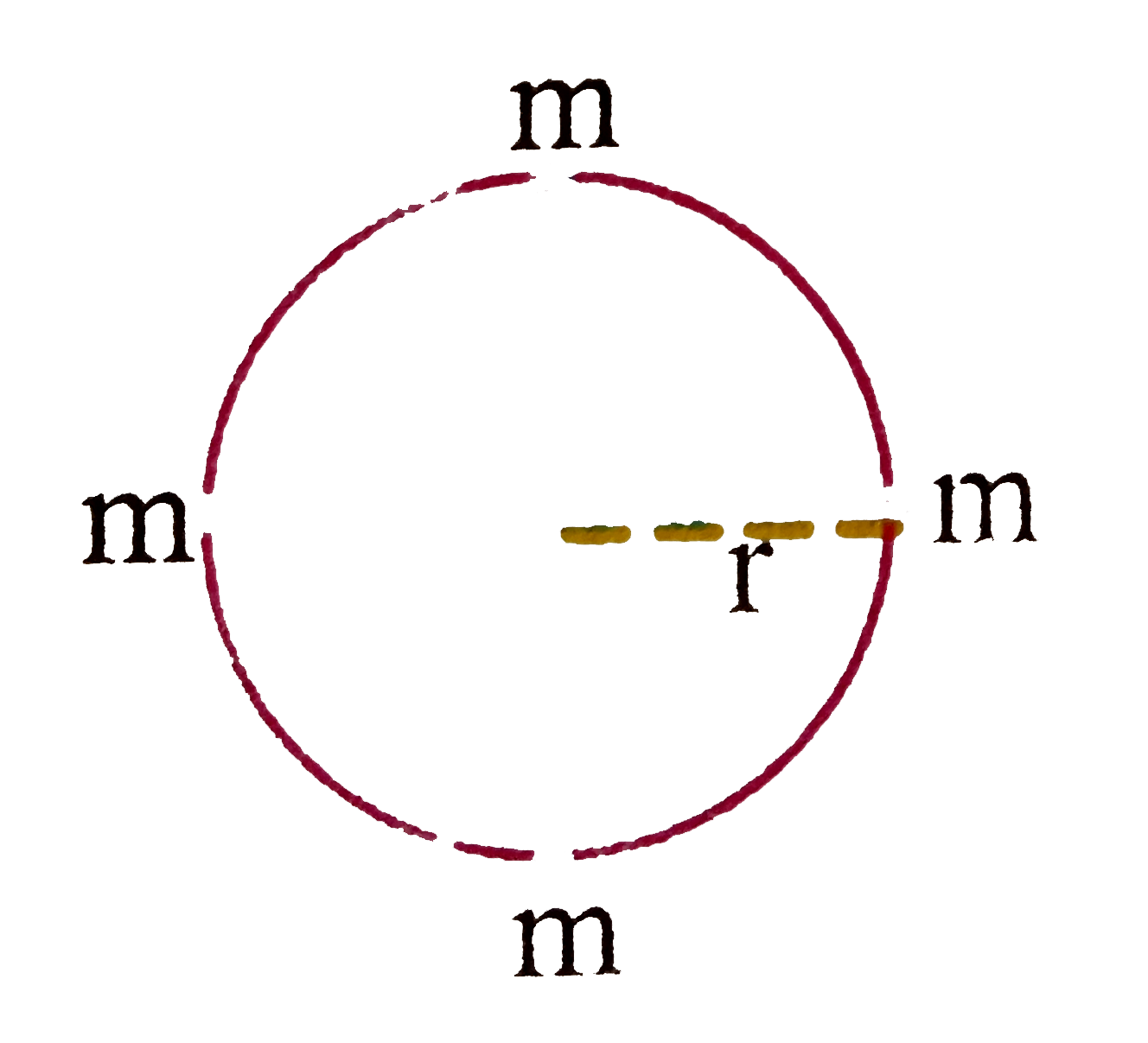
⎷Gmr(1+2√2)2
√Gmr
√Gmr(1+2√2)
⎷Gm2r(1+2√22)
The correct Answer is:C
Gm2(2r)2+2Gm2(√2r)2cos45=mv2r
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:NCERT BASED QUESTIONS
Explore 26 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL -I(H.W)
Explore 56 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL II (C.W.)
Explore 38 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.
View SolutionTwo masses on 1kg each are rotating in a circle of radius R under their gravitational force. Find their angular speed in terms of G and R
View Solution
Knowledge Check
Three particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
A√GM√2RB√GM√3RC√GM2RD√GM3RFour similar particles of mass m are orbiting in a circle of radius r in the same direction and same speed because of their mutual gravitational attractive force as shown in the figure . Speed of a particle is given by
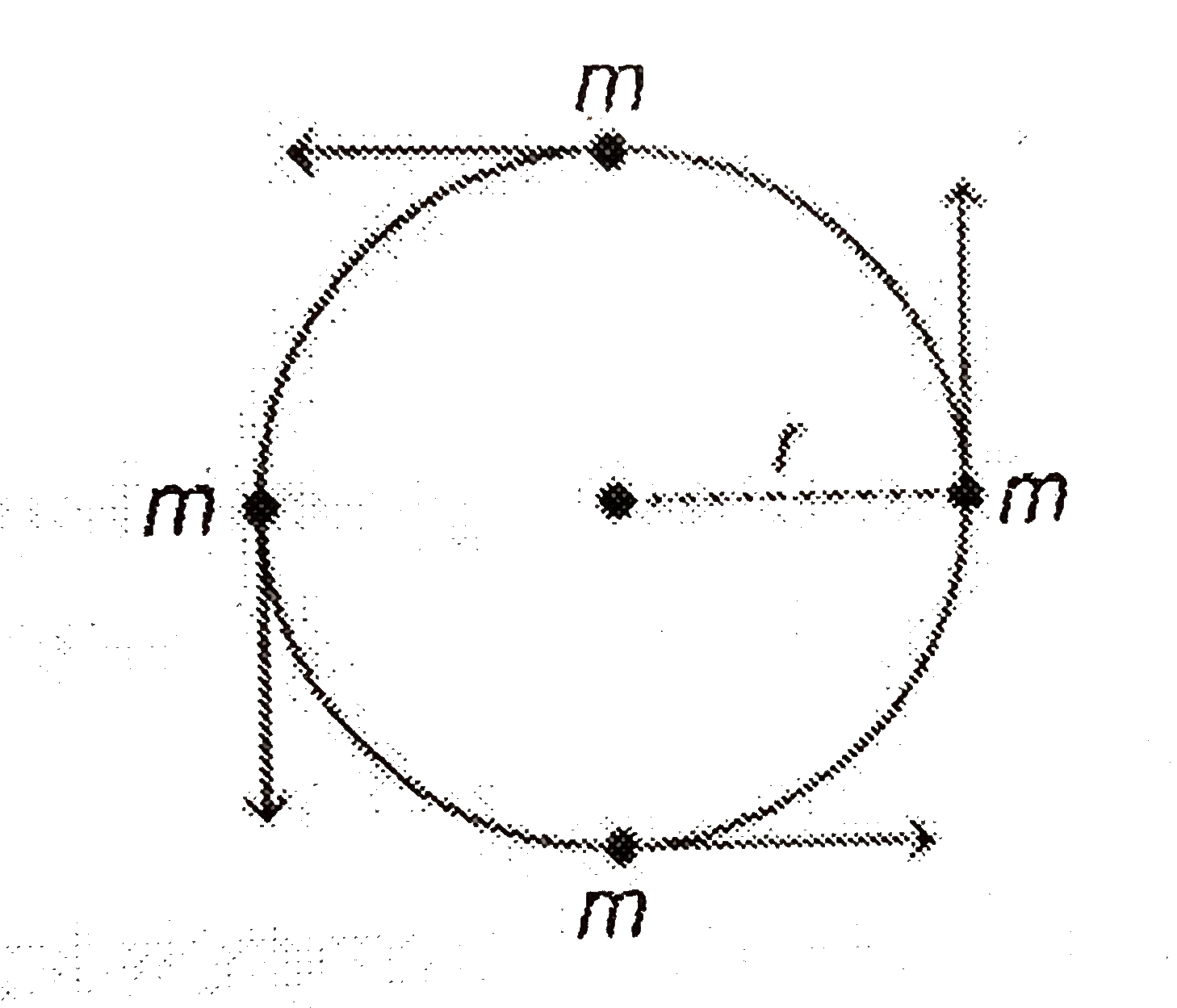 A√Gm4r(1+2√2)B√Gmr(1+√2)C√Gmr(1+2√2)D√Gm4r(2+√2)
A√Gm4r(1+2√2)B√Gmr(1+√2)C√Gmr(1+2√2)D√Gm4r(2+√2)Two identical particles of mass 1 kg each go round a circle of radius R, under the action of their mutual gravitational attraction. The angular speed of each particle is :
A√G2R3B12√GR3C12R√1GD√2GR3
Two particles of equal masses m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is v=√GmnR. Find the value of n.
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View SolutionTwo particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionTwo particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
View Solution

