Consider three concentric shells of masses M1,M2andM3 having radii a,b and c respectively are situated as shown in

Gravitational field at a point located at Q and P is
G(M1+M2)y2,G(M1+M2)y2
G(M1+M2+M3)Y2,G(M1+M2)x2
G(M1+M2+M3)a2,GM1a2
G(M1+M2+M3)C2,GM2b2
The correct Answer is:B
Gravitational field at an external point due to spherical shell of mass M is (GMr2) while at an internal point is zero
(i) Point Q is external to shell, M1,M2andM3 So, field at Q will be
EQ=GM1y2+GM2y2+GM3y2=Gy2(M1+M2+M3)
(ii) Field at P will be
Fp=GM1x2+GM2x2+0=Gx2(M1+M2).
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Check Point 10.4
Explore 10 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Check Point 10.5
Explore 20 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Check Point 10.2
Explore 20 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 11 Videos
Similar Questions
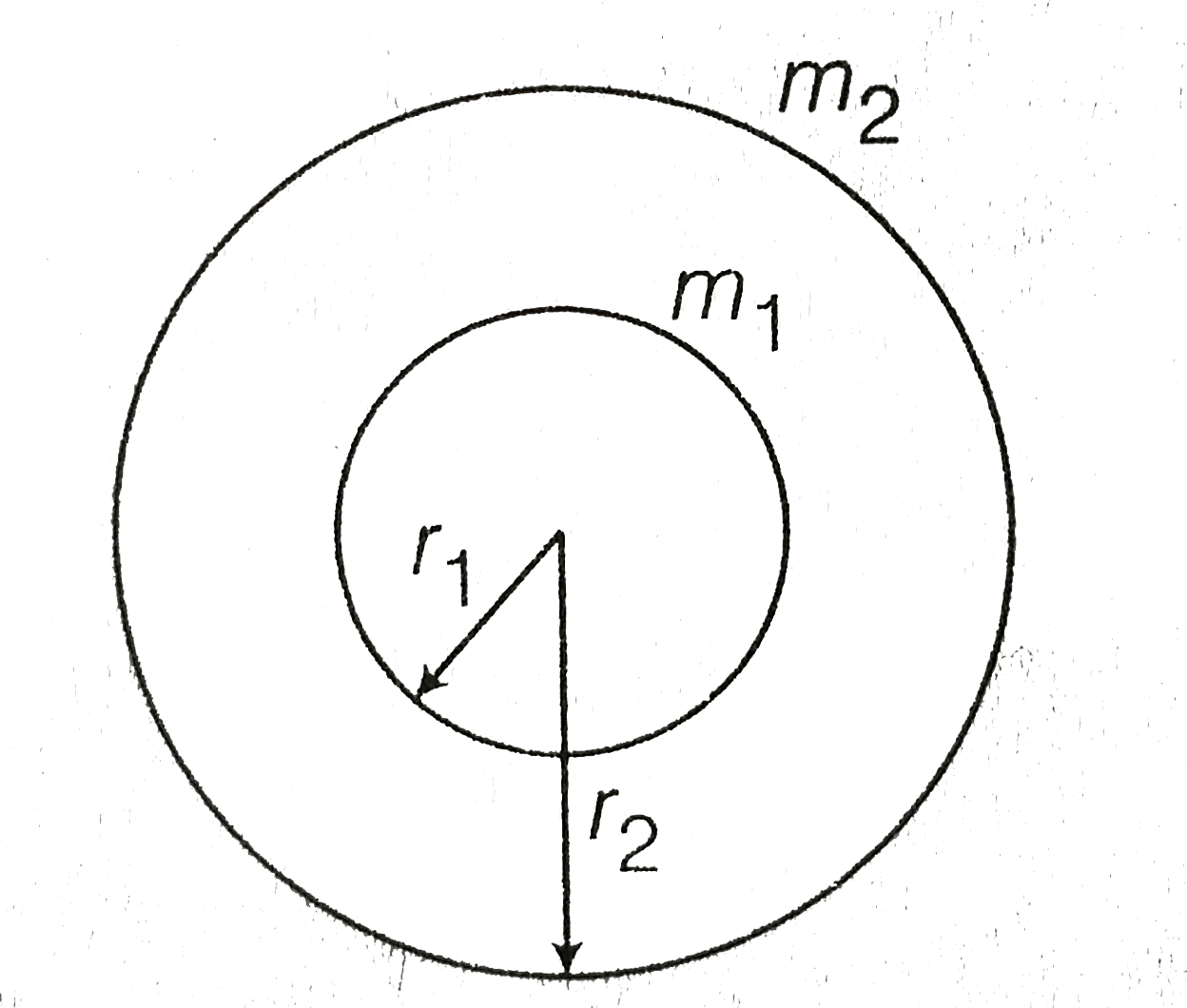
Two concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is

View SolutionTwo concentric shells of masses M1 and M2 are concentric as shown. Calculate the gravitational force on m due to M1 at points P,Q and R.

View Solution
Knowledge Check
Two concentric shells of masses M1 and M2 are having radii r1 and r2. Which of the following is the correct expression for the gravitational field on a mass m?
 AF=G(M1+M2)r2, for r<r1BF=G(M1+M2)(r2), for r<r2CF=GM2r2, for r1<r<r2DF=GM1r2, for r1<r<r2
AF=G(M1+M2)r2, for r<r1BF=G(M1+M2)(r2), for r<r2CF=GM2r2, for r1<r<r2DF=GM1r2, for r1<r<r2Two concentric shells have masses M and m and their radii are R and r, respectively, where R>r. What is the gravitational potential at their common centre?
A−GMRB−GMrC−G[MR−mr]D−G[MR+mr]The figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is
 AG(M1+M2)a2BGM1a2+GM2R22CGM1a2Dzero
AG(M1+M2)a2BGM1a2+GM2R22CGM1a2Dzero
Find the potential V at P in the gravitational field of fixed point mass M.
View SolutionTwo concentric spherical shells A and B of radii R and 2R and mases 4M, and M, respectively are placed in space as shown in Fig. The gravitational potential at P at a distance r(R<r<2R)from the centre of shells is

View SolutionThree concentric spherical shells A, B and C having uniformly distributed total charges +Q, -2Q and +Q respectively are placed as shown. The potential at the centre will be -
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View SolutionTwo bodies of masses M1 and M2 are kept separeated by a distance d. The potential at the point where the gravitational field produced by them is zero, is :-
View Solution

