Two concentric spherical shells A and B of radii R and 2R and mases 4M, and M, respectively are placed in space as shown in Fig. The gravitational potential at P at a distance r(R<r<2R)from the centre of shells is

−4GMR
−9GM2R
−4GM3R
none of these
The correct Answer is:D
Point P is outside the spherical shell A and inside the spherical shell B. So potential at point P is given by
VP= potential due to shell A
+ potential due to shell B
=−G×4Mr−GM2R=−GM[4r+12R]
Similar Questions
Two concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is

View SolutionTwo isolated concentric conducting spherical shells have radii R and 2R and uniform charges q and 2q respectively.If V1 and V2 are potentials at points located at distances 3R and R2 respectively from the centre of shells.Then the ratio of (V2V1) will be
View Solution
Knowledge Check
The figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is
 AG(M1+M2)a2BGM1a2+GM2R22CGM1a2Dzero
AG(M1+M2)a2BGM1a2+GM2R22CGM1a2DzeroTwo concentric shells have masses M and m and their radii are R and r, respectively, where R>r. What is the gravitational potential at their common centre?
A−GMRB−GMrC−G[MR−mr]D−G[MR+mr]Two concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
AzeroB(Q+q)rRC(Q−q)rRDqrR
A sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionTwo concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=14πɛ0)
View SolutionThree concentric spherical conductors A, B and C of radii R, 2R and 4R respectively. A and C is shorted and B is uniformly charged .
Potential at B is

View SolutionThree concentric conducting spherical shells of radii R,2R and 3R carry charges Q,−2Q and 3Q, respectively.
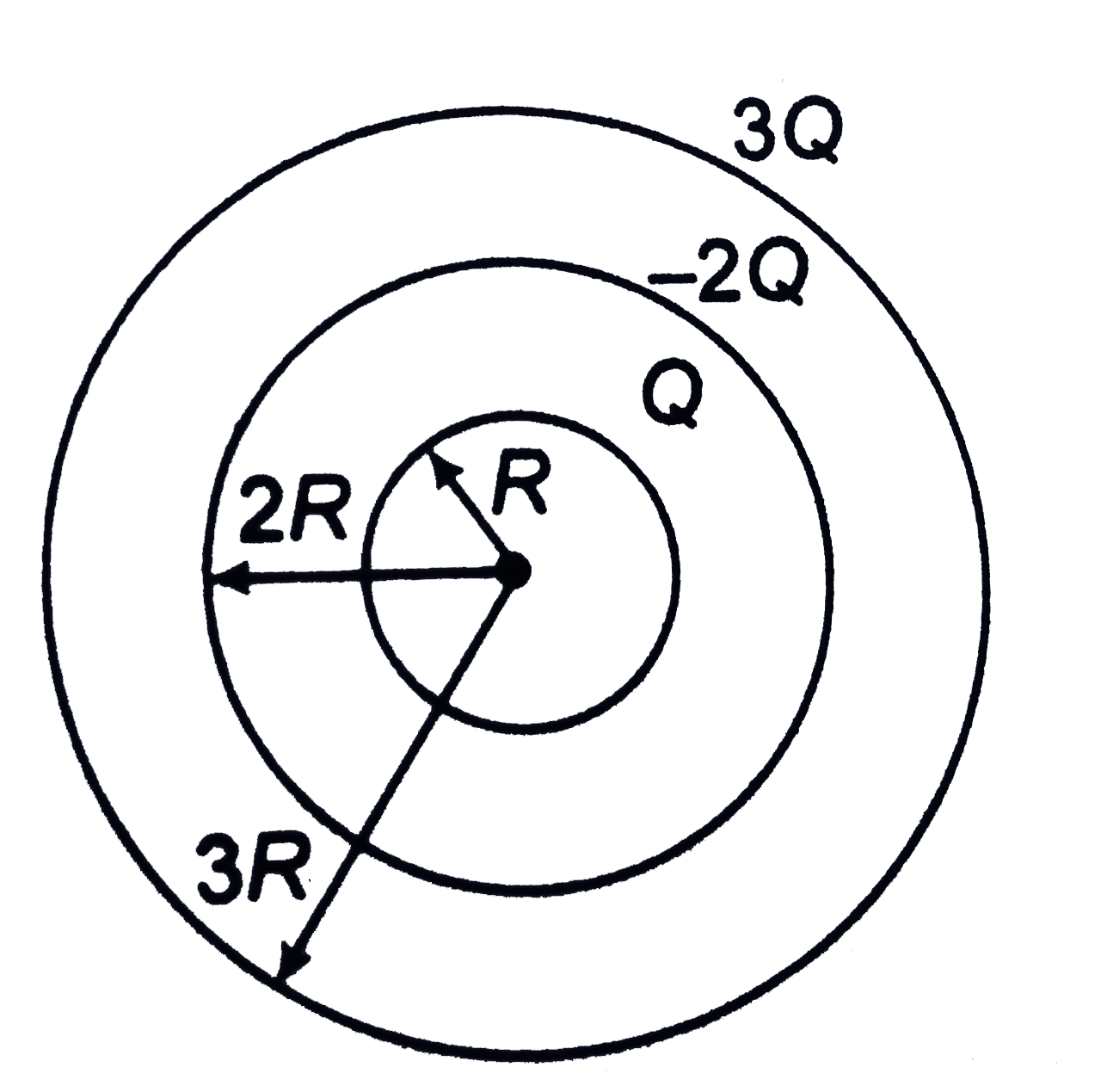
a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre. ltbr> b. Compute the electric field at r=52R
c.computethe→tale≤ctrostatice≠rgys→red∈thesystem.<br>The∈≠rshellisnowco∩ected→theexternalo≠byaconduct∈gwire,passingthroughaverysmallho≤∈them≤shell.<br>Computethechar≥sonthespheresofradiiRand3R.<br>e.Computethee≤ctricfieldatr=5/2R.
View SolutionTwo concentric spherical shells of radii R and 2R have charges Q and 2Q as shown in figure

If we draw a graph between potential V and distance r from the centre, the graph will be like
View Solution

