Find the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
To find the gravitational potential V due to a spherical shell of mass M and radius R, we will consider two cases: when the distance r from the center of the shell is less than R (i.e., r<R) and when r is greater than R (i.e., r>R).
Step 1: Gravitational Potential Inside the Shell (r<R)
1. Understanding the Shell Theorem: According to the Shell Theorem, a uniform spherical shell of mass exerts no gravitational force on any object located inside it. This means that the gravitational field g inside the shell is zero.
2. Finding the Gravitational Potential: The gravitational potential V is related to the gravitational field g by the equation:
V=−∫gdr
Since g=0 inside the shell, the potential V remains constant throughout the interior of the shell.
3. Calculating the Constant Potential: The value of the gravitational potential at the surface of the shell (where r=R) can be calculated using the formula for the gravitational potential due to a point mass:
V(R)=−GMR
Since the potential is constant inside the shell, we have:
V(r)=−GMRfor r<R
Step 2: Gravitational Potential Outside the Shell (r>R)
1. Using the Shell Theorem: For points outside the spherical shell, the shell can be treated as if all its mass were concentrated at its center. Thus, we can use the formula for the gravitational potential due to a point mass.
2. Calculating the Gravitational Potential: The gravitational potential V at a distance r from the center of the shell (where r>R) is given by:
V(r)=−GMr
Final Results
- For r<R:
V(r)=−GMR
- For r>R:
V(r)=−GMr
V=−∫gdr
Since g=0 inside the shell, the potential V remains constant throughout the interior of the shell.
V(R)=−GMR
Since the potential is constant inside the shell, we have:
V(r)=−GMRfor r<R
V(r)=−GMr
V(r)=−GMR
V(r)=−GMr
Topper's Solved these Questions
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Assigment problems (Subjective) (level I)
Explore 14 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Assigment problems (Subjective) (level II & III)
Explore 15 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Matrix match type
Explore 2 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
Similar Questions
A point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View SolutionUsing Gauss' law deduce the expression for the electric field due to uniformaly charged spherical conducting shell of radius R at point (i) outside ,and (ii) inside the shell.
Plot a graph showing variation of electric field as a functions or r for r< R and .(r being the distance from the centre of the shell).
View Solution
Knowledge Check
Which of the following graph represents the variation of electric field E due to a thin charged spherical shell of radius R as a function of the distance r from the centre of the shell?
A B
B CD
CD
Consider a thin spherical shell of uniform density of mass M and radius R:
AThe gravitational field inside the shell will be zeroBThe gravitational self energy of shell is GM22RCAttractive force experience by unit area of the shell pull the other half is GM22R2DNet gravitational force with which one hemisphere of the shell arracts other, is GM28R2Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).
A B
B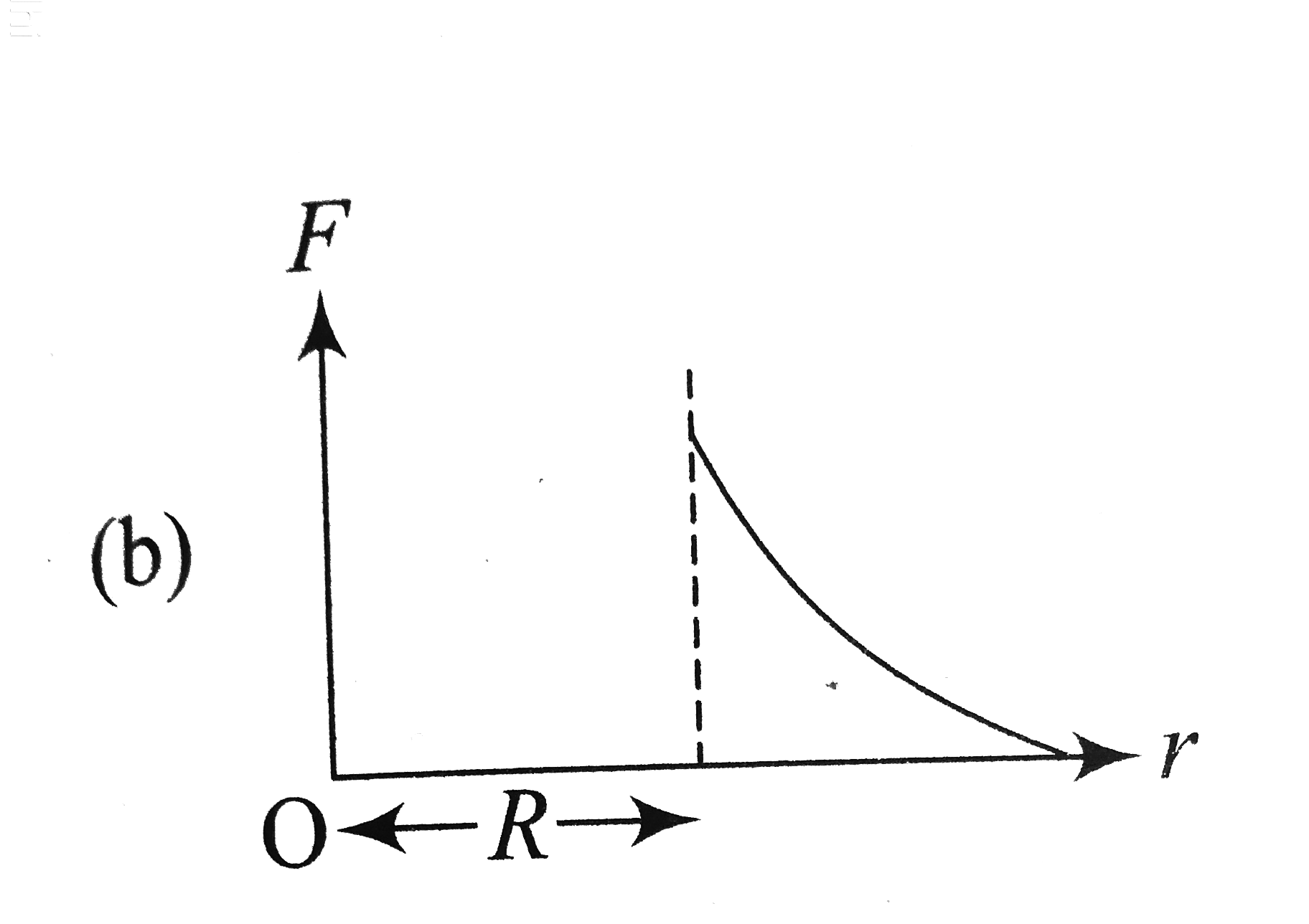 C
C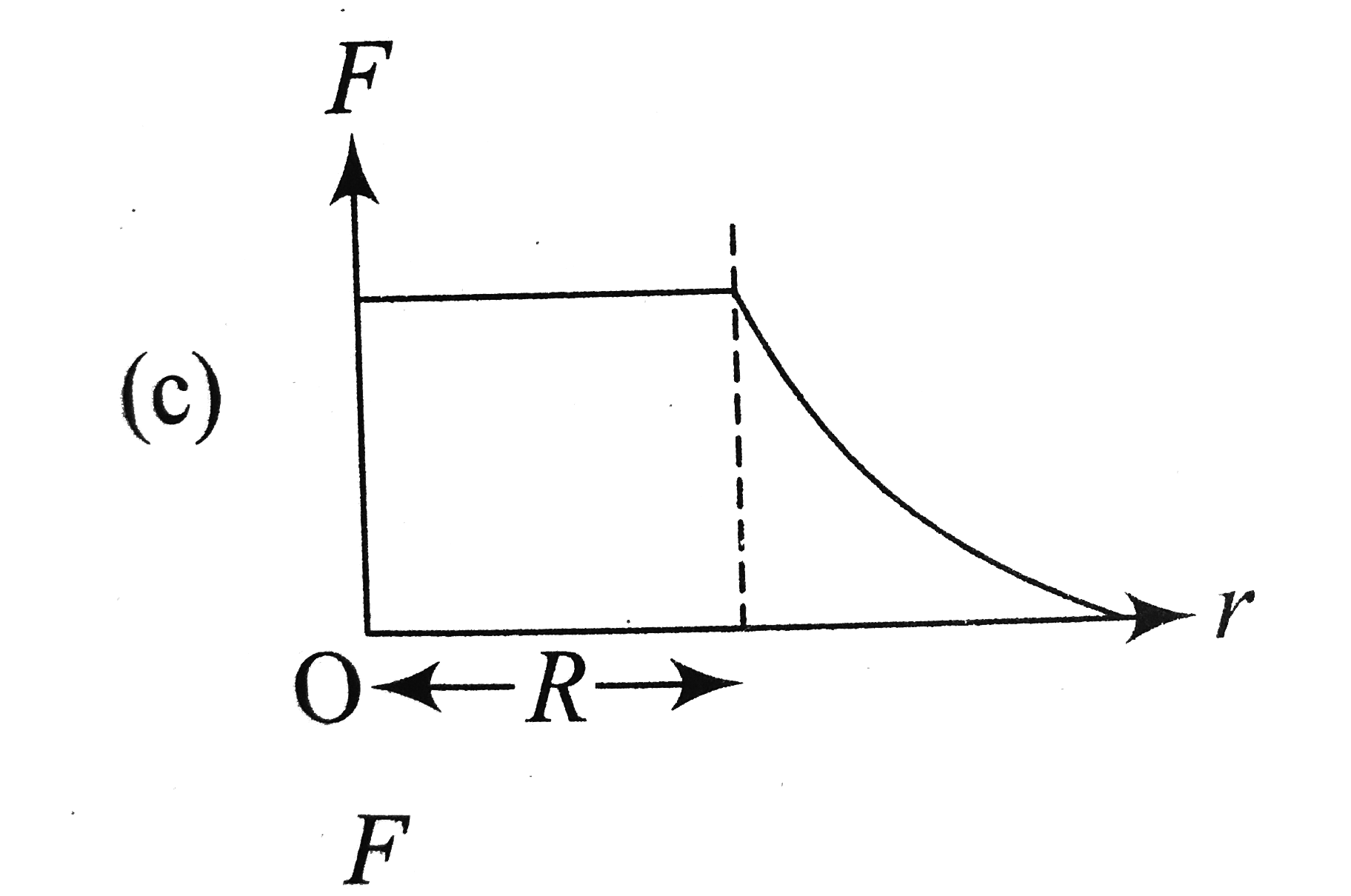 D
D
The electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionA point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R from the center of the shell. Find the electric potential at the center of the shell.
View SolutionA charge +q is placed somewhere inside the cavity of a thick conducting spherical shell of inner radius R1 and outer radius R2. A charge – Q is placed at a distance r>R2 from the centre of the shell. Then the electric field in the hollow cavity-
View SolutionA point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R fro the centre of the shell. The electric potential at the centre of shell will (potential at infinity is zero).
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
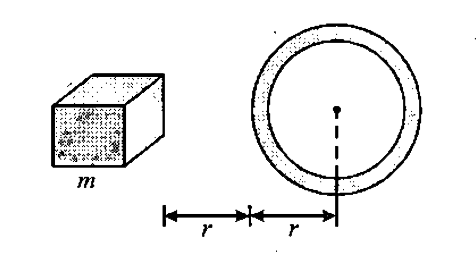
View Solution

